Spiel AOI Algorithmus Analyse und Leistungsprüfung
Einleitung
AOI (Area Of Interest) ist eine grundlegende Funktion in Mehrspielerspielen, bei der Spieler Informationen über andere Spieler oder Entitäten (Entity) erhalten, die in ihren Sichtbereich eintreten. Die Algorithmen, die berechnen, welche Entitäten sich im Sichtbereich eines Spielers befinden und welche Entitäten diesen Bereich betreten oder verlassen, nennen wir im Allgemeinen den AOI-Algorithmus.
Dieser Artikel behandelt zwei AOI-Algorithmen, das Neunfeldraster und die Kreuzverkettung, und bietet eine Leistungsanalyse der beiden Algorithmen aus praktischen Tests, damit du genau weißt, wie du sie einsetzen kannst, und in schwierigen Situationen ruhig bleibst.
Im Text werden die Begriffe Spieler und Entität erwähnt. Eine Entität ist das Konzept eines Objekts im Spiel, während der Spieler eine Entität ist, die über AOI verfügt.
Der Code im Text kann hier gefunden werden: AoiTesting。
Das heißt "Gitter" auf Deutsch.
Der Begriff "Nine Grid" bezieht sich darauf, dass die Positionen aller Entitäten in einer Szene in Gitter unterteilt werden, beispielsweise in Quadrate mit einer Seitenlänge von 200. Um andere Entitäten im AOI-Bereich des Zentralplayers zu finden, müssen alle Spieler untersucht werden, die sich in den Gittern dieses Bereichs befinden.
For example, in every 100 milliseconds, a tick occurs in the scene. During the tick, we can update the player's AOI in this way:
- Basierend auf der Position des Spielers umfasst die AOI-Radiusberechnung die Menge der betroffenen Felder. Berechnen Sie den Abstand jedes Elements aus der Gittersammlung zum Spieler. Die Menge der Entitäten, deren Abstand kleiner als der AOI-Radius ist, bildet den neuen AOI des Spielers.
Der Sudoku-Algorithmus ist einfach umzusetzen, er lässt sich in wenigen Sätzen klar beschreiben. Eine detaillierte Leistungsanalyse werden wir später durchführen, zunächst schauen wir uns den Kreuzketten-Algorithmus an.
Kreuzverkettete Liste
Für 3D-Spiele erstellen wir normalerweise geordnete Listen für die X- und Z-Achsenkoordinaten. Jede Entität hat einen Knoten in der Liste, der den Koordinatenwert enthält. Die Werte werden in aufsteigender Reihenfolge gespeichert. Wenn jedoch nur die Koordinatenpunkte der Entität gespeichert werden, ist die Effizienz der Abfrage in diesen beiden Listen immer noch sehr gering.
Das wirklich Entscheidende ist, dass wir in der verketteten Liste für jeden Spieler mit AOI zwei Wächterknoten hinzufügen, einen links und einen rechts. Die Koordinaten der beiden Wächter unterscheiden sich genau um den AOI-Radius von den Koordinaten des Spielers selbst. Zum Beispiel, wenn die Koordinaten des Spielers P (a, b, c) sind und der AOI-Radius r beträgt, dann gibt es auf der X-Achse zwei Wächter left_x und right_x, deren Koordinaten a - r und a + r sind. Durch das Vorhandensein der Wächter können wir die AOI aktualisieren, indem wir die Bewegung der Wächter und anderer Entitätsknoten verfolgen. Um das vorherige Beispiel fortzuführen: Wenn sich eine Entität E bewegt und somit auf der X-Achse vom rechten Bereich von left_x nach links über left_x hinweg in den linken Bereich von left_x gelangt, bedeutet das, dass E definitiv die AOI von P verlassen hat; ebenso, wenn sie nach rechts über right_x hinausgeht, verlässt sie ebenfalls die AOI. Im Gegensatz dazu, wenn sie nach rechts über left_x oder nach links über right_x überschreitet, könnte dies bedeuten, dass sie möglicherweise in die AOI von P eintritt.
Es ist zu erkennen, dass der Algorithmus der Kreuzliste viel komplexer ist als das Sudoku. Wir müssen zwei geordnete Listen pflegen und bei jeder Aktualisierung der Entitätskoordinaten die Knoten in der Liste synchron verschieben und AOI aktualisieren, wenn sie andere Knoten überqueren.
Die Umsetzung des Sudoku-Rasters
Da es sich um die tatsächliche Leistung handelt, lassen Sie uns zunächst etwas tiefer in die Implementierungsdetails des 3x3-Grid-Algorithmus eintauchen:
struct Sensor {
// ...
Nuid sensor_id;
float radius;
float radius_square;
PlayerPtrList aoi_players[2];
};
struct PlayerAoi {
// ...
Nuid nuid;
SquareId square_id;
int square_index;
Pos pos;
Pos last_pos;
Uint32 flags;
std::vector<Sensor> sensors;
};
PlayerAoi speichert die Daten der Spieler, darunter ein sensors Array, das zur Berechnung von Entitäten innerhalb eines bestimmten Bereichs dient. Nach jedem Tick werden die berechneten Entitäten im aoi_players geplant. aoi_players enthält zwei Arrays, die verwendet werden, um die Ergebnisse des vorherigen Ticks zu vergleichen und die Spieler zu ermitteln, die eingetreten oder ausgestiegen sind. Der grobe Ablauf eines Ticks ist wie folgt:
AoiUpdateInfos SquareAoi::Tick() {
AoiUpdateInfos update_infos;
PlayerPtrList remove_list;
for (auto& elem : player_map_) {
auto& player = *elem.second;
// ...
// Berechnung von Aoi für Spieler mit Sensoren
if (!player.sensors.empty()) {
auto update_info = _UpdatePlayerAoi(cur_aoi_map_idx_, &player);
if (!update_info.sensor_update_list.empty()) {
update_infos.emplace(update_info.nuid, std::move(update_info));
}
}
// ...
}
// ...
// Aufzeichnen der vorherigen Position des Spielers
for (auto& elem : player_map_) {
auto& player = *elem.second;
player.last_pos = player.pos;
}
cur_aoi_map_idx_ = 1 - cur_aoi_map_idx_;
return update_infos;
}
Die von Tick ausgeführten Aufgaben sind recht einfach. Es durchläuft die Spieler mit Sensoren und berechnet jeden einzelnen die Entitäten im Bereich des Sensors, also den AOI. last_pos wird verwendet, um zu überprüfen, ob eine Entität den AOI betreten oder verlassen hat. Der Code für _UpdatePlayerAoi sieht folgendermaßen aus:
AoiUpdateInfo SquareAoi::_UpdatePlayerAoi(Uint32 cur_aoi_map_idx, PlayerAoi* pptr) {
AoiUpdateInfo aoi_update_info;
aoi_update_info.nuid = pptr->nuid;
Uint32 new_aoi_map_idx = 1 - cur_aoi_map_idx;
for (auto& sensor : pptr->sensors) {
auto& old_aoi = sensor.aoi_players[cur_aoi_map_idx];
auto& new_aoi = sensor.aoi_players[new_aoi_map_idx];
(this->*calc_aoi_players_func_)(*pptr, sensor, &new_aoi);
SensorUpdateInfo update_info;
auto& enters = update_info.enters;
auto& leaves = update_info.leaves;
float radius_square = sensor.radius_square;
_CheckLeave(pptr, radius_square, old_aoi, &leaves);
_CheckEnter(pptr, radius_square, new_aoi, &enters);
if (enters.empty() && leaves.empty()) {
continue;
}
update_info.sensor_id = sensor.sensor_id;
aoi_update_info.sensor_update_list.push_back(std::move(update_info));
}
return aoi_update_info;
}
old_aoi ist die vorherige AOI, die durch den letzten Tick berechnet wurde, und new_aoi ist die AOI, die im aktuellen Tick berechnet werden muss. new_aoi wird ermittelt, indem alle Entitäten in der AOI-Reichweite durchsucht werden, um diejenigen auszuwählen, die sich innerhalb des AOI-Radius befinden. Anschließend werden die Funktionen _CheckLeave und _CheckEnter verwendet, um die Entitäten zu berechnen, die in diesem Tick die AOI verlassen oder betreten. Zum Beispiel, wenn die Entität last_pos in new_aoi nicht innerhalb der AOI-Reichweite ist, bedeutet dies, dass diese Entität in diesem Tick in die AOI-Reichweite eingetreten ist. Der spezifische Code kann in den Quelltexten eingesehen werden, hier wird nicht weiter darauf eingegangen.
Die Implementierung einer verketteten Liste.
Im Vergleich zum 3x3-Gitter ist die Implementierung der Kreuzlisten komplexer. Schauen wir uns zunächst die grundlegende Datenstruktur an:
struct CoordNode {
// ...
Uint8 type;
float value;
CoordNode *prev = nullptr;
CoordNode *next = nullptr;
PlayerAoi *pplayer;
Sensor *psensor;
};
KHASH_MAP_INIT_INT64(SensorHashMap, PlayerAoi*);
struct Sensor {
// ...
Nuid sensor_id;
float radius;
float radius_square;
PlayerAoi *pplayer;
CoordNode left_x;
CoordNode right_x;
CoordNode left_z;
CoordNode right_z;
PlayerPtrList aoi_players[2];
std::shared_ptr<khash_t(SensorHashMap)> aoi_player_candidates;
};
struct PlayerAoi {
// ...
Nuid nuid;
Pos pos;
Pos last_pos;
Uint32 flags;
CoordNode node_x;
CoordNode node_z;
std::vector<Sensor> sensors;
std::shared_ptr<boost::unordered_map<Nuid, std::vector<Nuid>>> detected_by;
};
Sensor und PlayerAoi haben einige Ähnlichkeiten mit dem 3x3-Raster, haben jedoch eine zusätzliche verkettete Liste namens CoordNode. CoordNode ist ein Knoten in der Liste und speichert den Typ und den Wert des Knotens selbst, wobei es drei Typen gibt: Spielerknoten, Sensor-Linksknoten und Sensor-Rechtsknoten.
Die meiste Arbeit bei einer verketteten Liste wird dafür verwendet, die Ordnung der Liste aufrechtzuerhalten:
Wenn ein Spieler beitritt, muss der Spielerknoten an eine geordnete Position verschoben werden und dabei gleichzeitig Ereignisse für das Betreten oder Verlassen anderer Spieler im AOI behandeln.
* Nachdem der Spieler die richtige Position erreicht hat, bewegen sich die Sensor-Links und -Rechts von der Vorder- und Rückseite des Spielers aus zur richtigen Position und verarbeiten die Ein- und Austrittsevents, die ausgelöst werden, wenn sie andere Spielernodes überschreiten.
* Wenn der Spieler sich bewegt, aktualisieren Sie die Koordinaten des Spielers und bewegen Sie den Spieler-Knoten sowie die Knoten Sensor nach links und rechts, um das Eintreten und Verlassen des AOI zu verarbeiten.
Der Code für den beweglichen Knoten lautet wie folgt. Jedes Mal, wenn ein Knoten überschritten wird, wird die Funktion MoveCross aufgerufen. Abhängig von der Bewegungsrichtung, dem beweglichen Knoten und dem Typ des überschrittenen Knotens entscheidet die Funktion MoveCross, ob der Knoten den AOI betritt oder verlässt.
void ListUpdateNode(CoordNode **list, CoordNode *pnode) {
float value = pnode->value;
if (pnode->next && pnode->next->value < value) {
// move right
auto cur_node = pnode->next;
while (1) {
MoveCross(MOVE_DIRECTION_RIGHT, pnode, cur_node);
if (!cur_node->next || cur_node->next->value >= value) break;
cur_node = cur_node->next;
}
ListRemove(list, pnode);
ListInsertAfter(list, cur_node, pnode);
} else if (pnode->prev && pnode->prev->value > value) {
// move left
auto cur_node = pnode->prev;
while (1) {
MoveCross(MOVE_DIRECTION_LEFT, pnode, cur_node);
if (!cur_node->prev || cur_node->prev->value <= value) break;
cur_node = cur_node->prev;
}
ListRemove(list, pnode);
ListInsertBefore(list, cur_node, pnode);
}
}
Die Bewegung der verketteten Liste ist ziemlich langsam und hat eine Komplexität von O(n), insbesondere wenn ein neuer Spieler in die Szene kommt. Der Spieler muss von weit entfernt allmählich zur richtigen Position bewegt werden, was eine große Menge an durchlaufenden Knoten erfordert und zu erheblichem Ressourcenverbrauch führt. Um die Leistung zu optimieren, können wir in der Szene fest installierte Leuchttürme platzieren. Diese Leuchttürme funktionieren ähnlich wie Spieler, speichern jedoch zusätzlich Daten in Bezug auf detected_by, um festzuhalten, welche Sensor-Bereiche die Wächterentität erfasst. Wenn ein Spieler zum ersten Mal in die Szene gelangt, beginnt er nicht mehr von den entferntesten Positionen, sondern sucht nach dem nächstgelegenen Leuchtturm. Der Spieler wird dann neben dem Leuchtturm eingefügt und kann durch die Daten in detected_by auf dem Leuchtturm schneller in den AOI-Bereich anderer Spieler gelangen, die mit dem Leuchtturm übereinstimmen. Anschließend erfolgt die Bewegung zur richtigen Position, wobei auch das Betreten und Verlassen berücksichtigt wird. Ebenso können Sensoren durch Vererbung der Daten der Leuchttürme optimiert werden, um sich von der Position der Leuchttürme zur richtigen Position zu bewegen. Diese beiden Optimierungsansätze können die Leistung bei der Einfügung von Spielern um mehr als das Doppelte verbessern.
Sensor hat auch eine HashMap namens aoi_player_candidates (hier wurde zu Leistungszwecken khashDie durch die Bewegung des Knotens ausgelöste AOI-Ereignis kann tatsächlich nur ein quadratisches Gebiet mit einer Seitenlänge von 2r auf der X-Z-Achse erfassen, nicht das, was wir im strengen Sinne als kreisförmiges Gebiet der AOI betrachten. Alle Entitäten innerhalb dieses quadratischen Gebiets werden in aoi_player_candidates aufgezeichnet und im Tick durchlaufen, um den AOI-Bereich innerhalb des kreisförmigen Gebiets zu berechnen, weshalb es als candidates bezeichnet wird.
Alle Operationen der Cross-Linked-Listen sind darauf ausgerichtet, die Entitäten in einem quadratischen Bereich, die sogenannten candidates, kontinuierlich zu warten. Die Operationen, die Tick in der Cross-Linked-Liste durchführt, sind fast identisch mit dem Neun-Felder-Raster, nur das Iterieren und Berechnen der candidates für den AOI unterscheiden sich. Die candidates im Neun-Felder-Raster sind die Entitäten in den Feldern, die vom AOI-Kreisbereich abgedeckt werden, während die Cross-Linked-Liste die Entitäten im quadratischen Bereich mit einer Kantenlänge von 2r definiert ist, die durch die linke und rechte Nachbarknoten des Sensors begrenzt wird. Qualitativ gesehen werden die candidates in den Cross-Linked-Listen normalerweise weniger sein als im Neun-Felder-Raster, was zu weniger Iterationen in Tick führt und somit eine bessere Leistung bringt. Allerdings verursacht die Cross-Linked-Liste zusätzlichen Leistungsverbrauch bei der Listenwartung. Die Gesamtleistung der beiden Ansätze ist daher noch unbekannt. Wir werden dies in den kommenden Tests genauer untersuchen.
Leistungstest
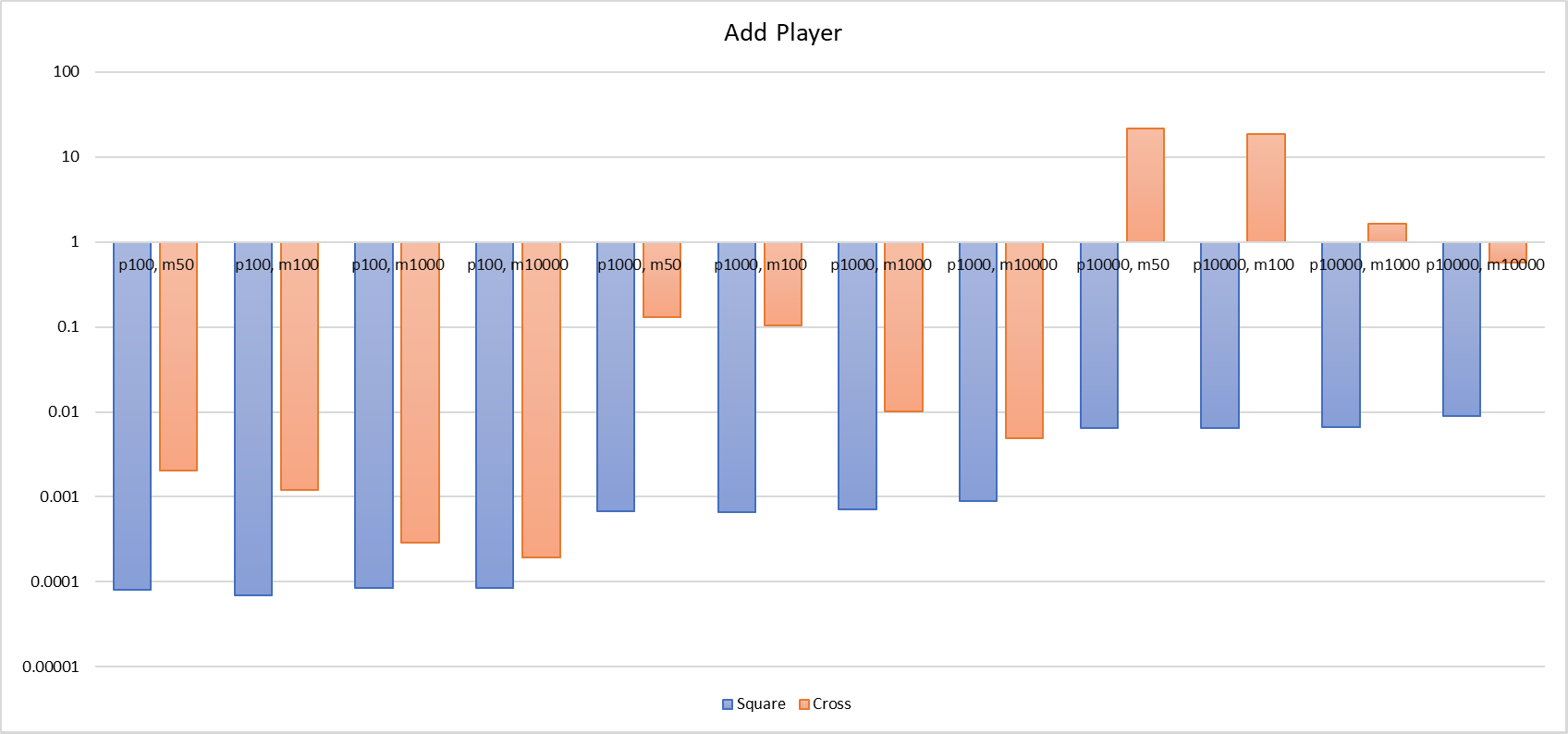
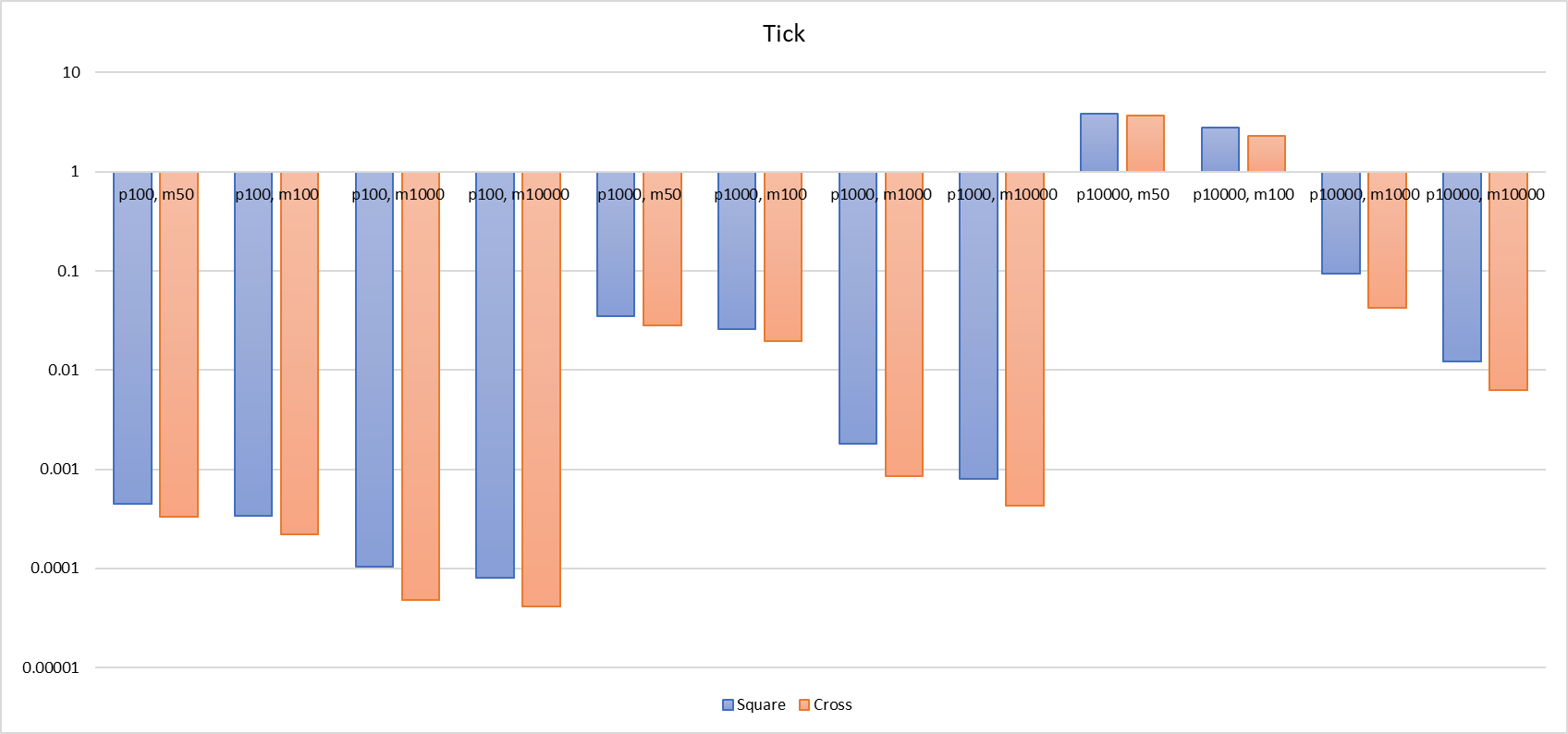
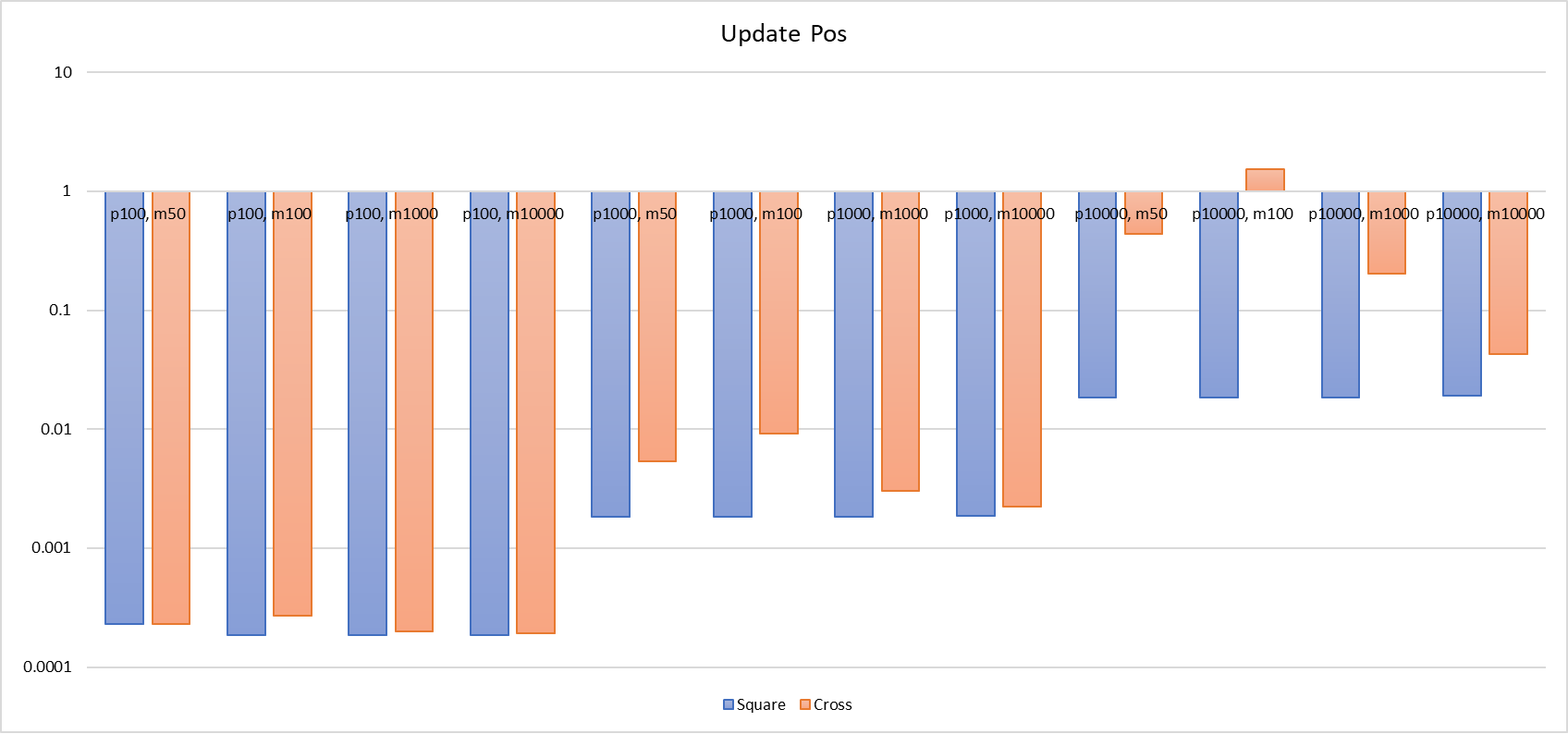
Ich habe jeweils die Zeit für drei Situationen gemessen: wenn ein Spieler dem Szenario beitritt („Spieler hinzufügen“), beim Berechnen von AOI-Eintritts- und Austrittsereignissen („Tick“) und wenn sich die Spielerposition aktualisiert („Position aktualisieren“).
Die Anfangsposition der Spieler wird zufällig innerhalb des Kartenbereichs generiert, gefolgt von der Hinzufügung der Spieler zur Szene. player_num ist die Anzahl der Spieler, während map_size den Bereich der X-Z-Koordinaten der Karte beschreibt. Die Position der Spieler wird gleichmäßig zufällig innerhalb dieses Bereichs generiert, wobei jeder Spieler einen Sensor mit einem Radius von 100 besitzt, der als AOI dient. Die Zeitberechnung erfolgt mit boost::timer::cpu_timer. Für player_num wurden die drei Werte 100, 1000, 10000 gewählt, während map_size die vier Werte [-50, 50], [-100, 100], [-1000, 1000], [-10000, 10000] umfasst.
Aktualisieren der Spielerposition wird den Spieler in einer festen zufälligen Richtung bewegen, mit einer Geschwindigkeit von 6m/s.
Die Testumgebung lautet:
- CPU: Intel(R) Core(TM) i5-4590 CPU @ 3.30GHz
- System: Debian GNU/Linux 10 (buster)
- gcc 版本: gcc Version 8.3.0 (Debian 8.3.0-6)
- Boost-Version: boost_1_75_0
Neun-Gitter-Test
Die Testergebnisse des Sudoku-Gitters sind wie folgt:
===Begin Milestore: player_num = 100, map_size = (-50.000000, 50.000000)
Add Player (1 times) 0.000081s wall, 0.000000s user + 0.000000s system = 0.000000s CPU (n/a%)
Tick (1 times) 0.000452s wall, 0.000000s user + 0.000000s system = 0.000000s CPU (n/a%)
Update Pos (10 times) 0.000230s wall, 0.000000s user + 0.000000s system = 0.000000s CPU (n/a%)
===End Milestore
===Begin Milestore: player_num = 100, map_size = (-100.000000, 100.000000)
Add Player (1 times) 0.000070s wall, 0.000000s user + 0.000000s system = 0.000000s CPU (n/a%)
Tick (1 times) 0.000338s wall, 0.000000s user + 0.000000s system = 0.000000s CPU (n/a%)
Update Pos (10 times) 0.000185s wall, 0.000000s user + 0.000000s system = 0.000000s CPU (n/a%)
===End Milestore
===Begin Milestore: player_num = 100, map_size = (-1000.000000, 1000.000000)
Add Player (1 times) 0.000084s wall, 0.000000s user + 0.000000s system = 0.000000s CPU (n/a%)
Tick (1 times) 0.000103s wall, 0.000000s user + 0.000000s system = 0.000000s CPU (n/a%)
Update Pos (10 times) 0.000187s wall, 0.000000s user + 0.000000s system = 0.000000s CPU (n/a%)
===End Milestore
===Begin Milestore: player_num = 100, map_size = (-10000.000000, 10000.000000)
Add Player (1 times) 0.000084s wall, 0.000000s user + 0.000000s system = 0.000000s CPU (n/a%)
Tick (1 times) 0.000080s wall, 0.000000s user + 0.000000s system = 0.000000s CPU (n/a%)
Update Pos (10 times) 0.000185s wall, 0.000000s user + 0.000000s system = 0.000000s CPU (n/a%)
===End Milestore
===Begin Milestore: player_num = 1000, map_size = (-50.000000, 50.000000)
Add Player (1 times) 0.000673s wall, 0.000000s user + 0.000000s system = 0.000000s CPU (n/a%)
Tick (1 times) 0.035298s wall, 0.030000s user + 0.000000s system = 0.030000s CPU (85.0%)
Update Pos (10 times) 0.001841s wall, 0.000000s user + 0.000000s system = 0.000000s CPU (n/a%)
===End Milestore
===Begin Milestore: player_num = 1000, map_size = (-100.000000, 100.000000)
Add Player (1 times) 0.000664s wall, 0.000000s user + 0.000000s system = 0.000000s CPU (n/a%)
Tick (1 times) 0.025806s wall, 0.030000s user + 0.000000s system = 0.030000s CPU (116.3%)
Update Pos (10 times) 0.001842s wall, 0.000000s user + 0.000000s system = 0.000000s CPU (n/a%)
===End Milestore
===Begin Milestore: player_num = 1000, map_size = (-1000.000000, 1000.000000)
Add Player (1 times) 0.000721s wall, 0.000000s user + 0.000000s system = 0.000000s CPU (n/a%)
Tick (1 times) 0.001793s wall, 0.000000s user + 0.000000s system = 0.000000s CPU (n/a%)
Update Pos (10 times) 0.001849s wall, 0.010000s user + 0.000000s system = 0.010000s CPU (540.8%)
===End Milestore
===Begin Milestore: player_num = 1000, map_size = (-10000.000000, 10000.000000)
Add Player (1 times) 0.000885s wall, 0.000000s user + 0.000000s system = 0.000000s CPU (n/a%)
Tick (1 times) 0.000804s wall, 0.000000s user + 0.000000s system = 0.000000s CPU (n/a%)
Update Pos (10 times) 0.001855s wall, 0.000000s user + 0.000000s system = 0.000000s CPU (n/a%)
===End Milestore
===Begin Milestore: player_num = 10000, map_size = (-50.000000, 50.000000)
Add Player (1 times) 0.006454s wall, 0.010000s user + 0.000000s system = 0.010000s CPU (154.9%)
Tick (1 times) 3.822028s wall, 3.800000s user + 0.020000s system = 3.820000s CPU (99.9%)
Update Pos (10 times) 0.018402s wall, 0.020000s user + 0.000000s system = 0.020000s CPU (108.7%)
===End Milestore
===Begin Milestore: player_num = 10000, map_size = (-100.000000, 100.000000)
Add Player (1 times) 0.006439s wall, 0.000000s user + 0.000000s system = 0.000000s CPU (n/a%)
Tick (1 times) 2.805551s wall, 2.760000s user + 0.040000s system = 2.800000s CPU (99.8%)
Update Pos (10 times) 0.018489s wall, 0.010000s user + 0.000000s system = 0.010000s CPU (54.1%)
===End Milestore
===Begin Milestore: player_num = 10000, map_size = (-1000.000000, 1000.000000)
Add Player (1 times) 0.006698s wall, 0.010000s user + 0.000000s system = 0.010000s CPU (149.3%)
Tick (1 times) 0.093759s wall, 0.100000s user + 0.000000s system = 0.100000s CPU (106.7%)
Update Pos (10 times) 0.018350s wall, 0.010000s user + 0.000000s system = 0.010000s CPU (54.5%)
===End Milestore
===Begin Milestore: player_num = 10000, map_size = (-10000.000000, 10000.000000)
Add Player (1 times) 0.009046s wall, 0.010000s user + 0.000000s system = 0.010000s CPU (110.6%)
Tick (1 times) 0.012091s wall, 0.010000s user + 0.000000s system = 0.010000s CPU (82.7%)
Update Pos (10 times) 0.019033s wall, 0.020000s user + 0.000000s system = 0.020000s CPU (105.1%)
===End Milestore
Beim Spielermenge von 100 sind die Zeiten für die drei Operationen sehr gering. Im Extremfall map_size = [-50, 50], befinden sich alle Spieler im AOI-Bereich zueinander, die Tick-Dauer beträgt etwa 0,4ms. Das Hinzufügen von Spielern zur Szene und die Aktualisierung der Koordinaten haben beide eine lineare Komplexität von O(player_num), die Leistungsfähigkeit ist daher recht gut. Bei player_num = 10000 und map_size = [-50, 50], wenn die Anzahl der Spieler 10.000 erreicht, können Add Player und Update Pos, aufgrund ihrer linearen Natur, in wenigen Millisekunden abgeschlossen werden. Doch die Tick-Dauer steigt auf 3,8s, was eine enorme CPU-Belastung darstellt und unbrauchbar ist. Bei 10.000 Spielern und einer Karten Größe von [-1000, 1000] beträgt die Tick-Zeit etwa 94ms. Falls die Tick-Frequenz gesenkt werden kann, beispielsweise auf zweimal pro Sekunde, wäre es immer noch in einem akzeptablen Bereich.
Kreuzverkettungstest
Die Testergebnisse der Kreuzverkettung sind wie folgt:
===Begin Milestore: player_num = 100, map_size = (-50.000000, 50.000000)
Add Player (1 times) 0.002057s wall, 0.000000s user + 0.000000s system = 0.000000s CPU (n/a%)
Tick (1 times) 0.000330s wall, 0.000000s user + 0.000000s system = 0.000000s CPU (n/a%)
Update Pos (10 times) 0.000232s wall, 0.000000s user + 0.000000s system = 0.000000s CPU (n/a%)
===End Milestore
===Begin Milestore: player_num = 100, map_size = (-100.000000, 100.000000)
Add Player (1 times) 0.001201s wall, 0.000000s user + 0.000000s system = 0.000000s CPU (n/a%)
Tick (1 times) 0.000222s wall, 0.000000s user + 0.000000s system = 0.000000s CPU (n/a%)
Update Pos (10 times) 0.000272s wall, 0.000000s user + 0.000000s system = 0.000000s CPU (n/a%)
===End Milestore
===Begin Milestore: player_num = 100, map_size = (-1000.000000, 1000.000000)
Add Player (1 times) 0.000288s wall, 0.000000s user + 0.000000s system = 0.000000s CPU (n/a%)
Tick (1 times) 0.000048s wall, 0.000000s user + 0.000000s system = 0.000000s CPU (n/a%)
Update Pos (10 times) 0.000200s wall, 0.000000s user + 0.000000s system = 0.000000s CPU (n/a%)
===End Milestore
===Begin Milestore: player_num = 100, map_size = (-10000.000000, 10000.000000)
Add Player (1 times) 0.000194s wall, 0.000000s user + 0.000000s system = 0.000000s CPU (n/a%)
Tick (1 times) 0.000041s wall, 0.000000s user + 0.000000s system = 0.000000s CPU (n/a%)
Update Pos (10 times) 0.000192s wall, 0.000000s user + 0.000000s system = 0.000000s CPU (n/a%)
===End Milestore
===Begin Milestore: player_num = 1000, map_size = (-50.000000, 50.000000)
Add Player (1 times) 0.130766s wall, 0.130000s user + 0.000000s system = 0.130000s CPU (99.4%)
Tick (1 times) 0.028091s wall, 0.020000s user + 0.000000s system = 0.020000s CPU (71.2%)
Update Pos (10 times) 0.005369s wall, 0.010000s user + 0.000000s system = 0.010000s CPU (186.2%)
===End Milestore
===Begin Milestore: player_num = 1000, map_size = (-100.000000, 100.000000)
Add Player (1 times) 0.103015s wall, 0.100000s user + 0.000000s system = 0.100000s CPU (97.1%)
Tick (1 times) 0.019545s wall, 0.020000s user + 0.000000s system = 0.020000s CPU (102.3%)
Update Pos (10 times) 0.009208s wall, 0.010000s user + 0.000000s system = 0.010000s CPU (108.6%)
===End Milestore
===Begin Milestore: player_num = 1000, map_size = (-1000.000000, 1000.000000)
Add Player (1 times) 0.010150s wall, 0.010000s user + 0.000000s system = 0.010000s CPU (98.5%)
Tick (1 times) 0.000845s wall, 0.000000s user + 0.000000s system = 0.000000s CPU (n/a%)
Update Pos (10 times) 0.003023s wall, 0.000000s user + 0.000000s system = 0.000000s CPU (n/a%)
===End Milestore
===Begin Milestore: player_num = 1000, map_size = (-10000.000000, 10000.000000)
Add Player (1 times) 0.004950s wall, 0.010000s user + 0.000000s system = 0.010000s CPU (202.0%)
Tick (1 times) 0.000427s wall, 0.000000s user + 0.000000s system = 0.000000s CPU (n/a%)
Update Pos (10 times) 0.002234s wall, 0.000000s user + 0.000000s system = 0.000000s CPU (n/a%)
===End Milestore
===Begin Milestore: player_num = 10000, map_size = (-50.000000, 50.000000)
Add Player (1 times) 21.606402s wall, 21.040000s user + 0.570000s system = 21.610000s CPU (100.0%)
Tick (1 times) 3.696885s wall, 3.680000s user + 0.030000s system = 3.710000s CPU (100.4%)
Update Pos (10 times) 0.434396s wall, 0.430000s user + 0.000000s system = 0.430000s CPU (99.0%)
===End Milestore
===Begin Milestore: player_num = 10000, map_size = (-100.000000, 100.000000)
Add Player (1 times) 18.499235s wall, 18.470000s user + 0.020000s system = 18.490000s CPU (100.0%)
Tick (1 times) 2.292608s wall, 2.290000s user + 0.000000s system = 2.290000s CPU (99.9%)
Update Pos (10 times) 1.522617s wall, 1.530000s user + 0.000000s system = 1.530000s CPU (100.5%)
===End Milestore
===Begin Milestore: player_num = 10000, map_size = (-1000.000000, 1000.000000)
Add Player (1 times) 1.642519s wall, 1.640000s user + 0.000000s system = 1.640000s CPU (99.8%)
Tick (1 times) 0.042767s wall, 0.050000s user + 0.000000s system = 0.050000s CPU (116.9%)
Update Pos (10 times) 0.202949s wall, 0.200000s user + 0.000000s system = 0.200000s CPU (98.5%)
===End Milestore
===Begin Milestore: player_num = 10000, map_size = (-10000.000000, 10000.000000)
Add Player (1 times) 0.571257s wall, 0.570000s user + 0.000000s system = 0.570000s CPU (99.8%)
Tick (1 times) 0.006325s wall, 0.010000s user + 0.000000s system = 0.010000s CPU (158.1%)
Update Pos (10 times) 0.042568s wall, 0.040000s user + 0.000000s system = 0.040000s CPU (94.0%)
===End Milestore
Wenn wir eine Analyse machen, dauert es bei der Hex-Liste länger für Add Player und Update Pos, besonders bei Add Player. Im Vergleich zur Gitterliste ist die Leistung um Hunderte oder sogar Tausende Male schlechter (100, [-50, 50] Hex-Liste braucht 2ms, während die Gitterliste nur 0,08ms benötigt; 10000, [-50, 50] Hex-Liste braucht 21,6s, die Gitterliste nur 6ms). Die Dauer von Update Pos kann auch um ein Vielfaches unterschiedlich sein, 10000, [-100, 100] Hex-Liste braucht 1,5s zur Aktualisierung der Spielerposition, während die Gitterliste nur 18ms benötigt. Es ist offensichtlich, dass bei der Hex-Liste die oberen und unteren Grenzen der Zeit, die für Add Player und Update Pos benötigt werden, größer sind als bei der Gitterliste. Sie sind stärker von der Anzahl der Spieler und der Größe der Karte abhängig. In dicht besiedelten Gebieten wird die Leistung dieser beiden Vorgänge stark beeinträchtigt, bis sie unbrauchbar werden.
Im Vergleich zur Tick-Operation der Kreuzkette ist die Gesamtleistung tatsächlich besser als die des 3x3-Rasters. Im besten Fall dauert es nur etwa die Hälfte der Zeit des 3x3-Rasters (bei 1000, [-1000, 1000] benötigt die Kreuzkette 0,8 ms, das 3x3-Raster 1,8 ms). Allerdings kann die Kreuzkette im schlechtesten Fall in die Nähe der Leistung des 3x3-Rasters zurückfallen (bei 10000, [-10000, 10000] benötigt die Kreuzkette 3,7 s, das 3x3-Raster 3,8 s). Das liegt daran, dass die Szenen klein sind und die Spieler sich alle innerhalb der AOI-Bereiche des anderen befinden, sodass die Anzahl der candidates, die die Kreuzkette bei Tick durchläuft, tatsächlich schon sehr nah an der des 3x3-Rasters ist.
Der Kreuz-Kettenmechanismus muss besser als das 3x3-Gitter sein. Dafür sind einige stärkere Annahmen erforderlich, wie zum Beispiel bei einer Anzahl von 1000 Spielern und einer Kartenfläche von [-1000, 1000], beträgt die Zeit, die ein Tick in der Kreuz-Kettenmechanismus nimmt, 0,8ms, im 3x3-Gitter 1,8ms, die Aktualisierung der Position in der Kreuz-Kettenmechanismus braucht 0,3ms, im 3x3-Gitter 0,18ms (Achten Sie darauf, dass die Zeit für die Aktualisierung der Position die Summe der Zeiten für 10 mal Durchführung ist). Bei der Gesamtzeit von Tick + Update Pos darf die Anzahl der Update Pos-Aktualisierungen in der Kreuz-Kettenmechanismus nicht mehr als 8 Mal den Tick überschreiten, oder anders gesagt, zwischen zwei Tick-Operationen sollte die Anzahl der Update Pos-Aktualisierungen weniger als 8 Mal erfolgen. Außerdem ist der Prozess für das Hinzufügen von Spielern in der Kreuz-Kettenmechanismus sehr aufwändig und daher nicht für Szenarien geeignet, in denen Spieler häufig kurz hintereinander in oder aus Szenen eintreten oder in Szenen weit teleportiert werden. Darüber hinaus kann eine große Anzahl von Spielern, die kurz hintereinander in eine Szene eintreten, leicht zu einer Leistungsverschlechterung führen und die CPU stark belasten.
Für die Kreuzverkettungsliste kann unter einer Voraussetzung eine Optimierung vorgenommen werden: das Entfernen von Tick, vorausgesetzt, das Spiel akzeptiert quadratische AOIs und die zusätzlich zu den Quadrat-AOIs entstehenden Kosten in Bezug auf das Netzwerk sind akzeptabel. Diese Voraussetzung ist jedoch relativ streng, denn in Spielen nimmt der CPU-Verbrauch durch die AOI-Berechnung normalerweise nicht viel Platz ein. Wenn man jedoch runde AOIs in quadratische AOIs umwandelt, kann dies die Fläche der AOI vergrößern und die Anzahl der Spieler im Bereich erhöhen, sodass die Spielerzahl bei gleichmäßiger Verteilung möglicherweise um das 1,27-Fache ansteigt. Sollte diese Voraussetzung jedoch erfüllt sein, kann die Kreuzverkettungsliste auf eine regelmäßige Aktualisierung von AOI-Ereignissen ohne Tick verzichten, da die candidates der Kreuzverkettungsliste bereits ein quadratisches AOI verwalten, das ursprünglich nur zur Berechnung des runden AOIs diente, wobei man gezwungen war, im Tick zusätzlich die Abstände zu berechnen. In diesem Fall könnte die Kreuzverkettungsliste eine ausgezeichnete Leistung erzielen, denn die Leistung des Update Pos der Kreuzverkettungsliste kann um mehrere bis zu Dutzende von Malen im Vergleich zum Tick variieren.
Bitte geben Sie schließlich ein Säulendiagramm mit dem Vergleich beider.
Zusammenfassung
In this article, we introduced the principles and basic implementations of two AOI algorithms (Nine-patch and Cross-link), and analyzed the performance advantages and disadvantages of these two algorithms through measured data, hoping to provide readers with some help or inspiration.
Im Allgemeinen ist die Nine-Cell-Methode einfach umzusetzen und ermöglicht eine ausgewogene Leistung, ohne große Probleme. Sie ist besonders gut geeignet für AOI-Spiele, bei denen die Leistung nicht zum Engpass wird. Die Leistungsschwankungen der Nine-Cell-Methode liegen in einem erwartbaren Rahmen und die Mindestleistung ist ziemlich hoch, sodass sie nicht leicht zum Engpass führt. Auf der anderen Seite bietet sie jedoch wenig Optimierungsspielraum und die Zeitkomplexität ist relativ fest. Im Gegensatz dazu ist die Cross-Chain-Methode komplexer in der Umsetzung und bietet eine niedrigere Mindestleistung im Vergleich zur Nine-Cell-Methode. Allerdings kann die Cross-Chain-Methode, wenn bestimmte Annahmen und Voraussetzungen erfüllt sind, einen höheren Optimierungsspielraum bieten, oder anders ausgedrückt, ein höheres Potenzial haben. Beide Methoden haben Vor- und Nachteile, und in der Spieleindustrie haben verschiedene Engines sich für eine der beiden entschieden, je nach Bedarf und Meinung.
Meine Fähigkeiten sind begrenzt, der Inhalt des Textes spiegelt lediglich meine Gedanken wider. Bei Unzulänglichkeiten oder Ungereimtheiten bin ich offen für Kommentare und Diskussionen.
Original: https://wiki.disenone.site/de
This post is protected by CC BY-NC-SA 4.0 agreement, should be reproduced with attribution.
Visitors. Total Visits. Page Visits.
(https://github.com/disenone/wiki_blog/issues/new)Bitte weisen Sie auf alle ausgelassenen Stellen hin.