Analisis y pruebas de rendimiento del algoritmo AOI de juegos
引子
El AOI (Área de Interés) es una función básica en los juegos en línea multijugador, donde los jugadores necesitan recibir información sobre otros jugadores o entidades que ingresen al alcance de su visión. El cálculo de qué entidades se encuentran dentro del campo de visión de un jugador, así como los algoritmos que determinan qué entidades entran o salen de su campo de visión, se conocen comúnmente como algoritmos de AOI.
Este texto discute dos algoritmos AOI: la cuadrícula de 9 celdas y la cadena de 10 células, y ofrece un análisis de rendimiento práctico de ambos algoritmos para que puedas utilizarlos con confianza y mantener la calma en cualquier situación.
En el texto se mencionarán dos términos: jugador y entidad. Entidad es el concepto de objeto en el juego, mientras que jugador es la entidad que posee AOI.
El código mencionado en el texto se puede encontrar aquí: AoiTestingLo siento, pero no hay texto para traducir. ¿Hay algo más en lo que pueda ayudarte?
Nueve casillas
所谓九宫格,是把场景内所有实体的位置按照格子划分,譬如划分成边长 200 的正方形,要找出中心玩家 AOI 范围内的其他实体,就把这个范围内涉及到的格子内的玩家都做一遍比较。
Por ejemplo, en cada escena que pasa cada 100 milisegundos, hacemos un "tick", y en este "tick" podemos actualizar el Área de Interés (AOI) del jugador de la siguiente manera:
Calcular el conjunto de casillas involucradas en el radio AOI, con la posición del jugador como centro. Calcular la distancia entre cada entidad en un conjunto de cuadrículas y el jugador. El conjunto de entidades cuya distancia es menor que el radio de AOI es el nuevo AOI del jugador.
El algoritmo de la cuadrícula 3x3 es bastante simple de implementar; se puede describir con solo unas pocas frases. La análisis de rendimiento específico lo dejaremos para más adelante, primero echemos un vistazo al algoritmo de lista enlazada cruzada.
Lista enlazada doble
Para juegos en 3D, generalmente construimos listas encadenadas ordenadas para los ejes X y Z, donde cada entidad tiene un nodo en la lista que almacena el valor de ese eje, organizados en orden creciente. Sin embargo, si solo almacenamos los puntos de coordenadas de las entidades, la eficiencia de consulta de estas dos listas encadenadas sigue siendo muy baja.
Lo verdaderamente crucial es que en la lista enlazada vamos a agregar dos nodos centinelas a cada jugador que tiene un AOI. Los dos nodos centinelas tienen coordenadas que difieren exactamente en el radio de AOI de las coordenadas del jugador en sí. Por ejemplo, si las coordenadas del jugador P son (a, b, c) y el radio de AOI es r, entonces en el eje X habrá dos nodos centinelas, izquierdo_x y derecho_x, con coordenadas a - r y a + r, respectivamente. Debido a la presencia de los centinelas, actualizamos el AOI rastreando los movimientos de los centinelas y otros nodos de entidad. Siguiendo el ejemplo anterior, si una entidad E se mueve y cruza desde la derecha de left_x hacia la izquierda sobre left_x y llega al lado izquierdo de left_x, entonces E definitivamente ha salido del AOI de P; de manera similar, si cruza hacia la derecha de right_x, también sale del AOI. Por el contrario, si cruza hacia la derecha de left_x o hacia la izquierda de right_x, es posible que entre en el AOI de P.
Se puede observar que el algoritmo de lista en cruz es mucho más complejo que el de cuadrícula de nueve celdas. Necesitamos mantener dos listas ordenadas y, al actualizar las coordenadas de cada entidad, mover sincrónicamente los nodos en las listas, actualizando también el Área de Interés (AOI) al atravesar otros nodos.
Implementación del cuadrado mágico
Debido a la implicación de pruebas de rendimiento, vamos a adentrarnos un poco más en los detalles de implementación del algoritmo de la cuadrícula de nueve casillas.
struct Sensor {
// ...
Nuid sensor_id;
float radius;
float radius_square;
PlayerPtrList aoi_players[2];
};
struct PlayerAoi {
// ...
Nuid nuid;
SquareId square_id;
int square_index;
Pos pos;
Pos last_pos;
Uint32 flags;
std::vector<Sensor> sensors;
};
PlayerAoi almacena los datos de los jugadores, que incluyen una matriz llamada sensores utilizada para calcular entidades dentro de un rango específico. Después de cada Tick, las entidades calculadas se colocan en aoi_players. Esta última es una estructura que contiene dos matrices usadas para comparar los resultados del Tick anterior y determinar qué jugadores han entrado o salido. El proceso general de Tick es el siguiente:
AoiUpdateInfos SquareAoi::Tick() {
AoiUpdateInfos update_infos;
PlayerPtrList remove_list;
for (auto& elem : player_map_) {
auto& player = *elem.second;
// ...
// Calcular Aoi para jugadores con sensores
if (!player.sensors.empty()) {
auto update_info = _UpdatePlayerAoi(cur_aoi_map_idx_, &player);
if (!update_info.sensor_update_list.empty()) {
update_infos.emplace(update_info.nuid, std::move(update_info));
}
}
// ...
}
// ...
// Registrar la última posición del jugador
for (auto& elem : player_map_) {
auto& player = *elem.second;
player.last_pos = player.pos;
}
cur_aoi_map_idx_ = 1 - cur_aoi_map_idx_;
return update_infos;
}
Tick hace cosas simples, recorre a los jugadores con sensors y calcula uno por uno las entidades dentro del rango del sensor, lo que se conoce como AOI. last_pos se utiliza para determinar si una entidad ha entrado o salido del AOI, el código de _UpdatePlayerAoi es el siguiente:
AoiUpdateInfo SquareAoi::_UpdatePlayerAoi(Uint32 cur_aoi_map_idx, PlayerAoi* pptr) {
AoiUpdateInfo aoi_update_info;
aoi_update_info.nuid = pptr->nuid;
Uint32 new_aoi_map_idx = 1 - cur_aoi_map_idx;
for (auto& sensor : pptr->sensors) {
auto& old_aoi = sensor.aoi_players[cur_aoi_map_idx];
auto& new_aoi = sensor.aoi_players[new_aoi_map_idx];
(this->*calc_aoi_players_func_)(*pptr, sensor, &new_aoi);
SensorUpdateInfo update_info;
auto& enters = update_info.enters;
auto& leaves = update_info.leaves;
float radius_square = sensor.radius_square;
_CheckLeave(pptr, radius_square, old_aoi, &leaves);
_CheckEnter(pptr, radius_square, new_aoi, &enters);
if (enters.empty() && leaves.empty()) {
continue;
}
update_info.sensor_id = sensor.sensor_id;
aoi_update_info.sensor_update_list.push_back(std::move(update_info));
}
return aoi_update_info;
}
old_aoi es el AOI calculado en el último Tick, y new_aoi es el AOI que se necesita calcular en este Tick. new_aoi selecciona entidades dentro del rango de AOI cuya distancia al jugador sea menor que el radio de AOI, recorriendo todas las celdas en el rango de AOI. Luego, usando las funciones _CheckLeave y _CheckEnter, se calculan las entidades que salen e ingresan al AOI en este Tick. Por ejemplo, si la posición last_pos de una entidad en new_aoi no está dentro del rango de AOI, significa que esa entidad entró al rango de AOI en este Tick. Para ver el código específico, se puede consultar el archivo fuente, ya que aquí no entraremos en más detalles.
La implementación de una lista cruzada.
En comparación con el cuadrado mágico, la implementación de la lista enlazada cruzada es más compleja. Empecemos por ver la estructura de datos básica:
struct CoordNode {
// ...
Uint8 type;
float value;
CoordNode *prev = nullptr;
CoordNode *next = nullptr;
PlayerAoi *pplayer;
Sensor *psensor;
};
KHASH_MAP_INIT_INT64(SensorHashMap, PlayerAoi*);
struct Sensor {
// ...
Nuid sensor_id;
float radius;
float radius_square;
PlayerAoi *pplayer;
CoordNode left_x;
CoordNode right_x;
CoordNode left_z;
CoordNode right_z;
PlayerPtrList aoi_players[2];
std::shared_ptr<khash_t(SensorHashMap)> aoi_player_candidates;
};
struct PlayerAoi {
// ...
Nuid nuid;
Pos pos;
Pos last_pos;
Uint32 flags;
CoordNode node_x;
CoordNode node_z;
std::vector<Sensor> sensors;
std::shared_ptr<boost::unordered_map<Nuid, std::vector<Nuid>>> detected_by;
};
Sensor y PlayerAoi son en cierta medida similares al juego del Sudoku, pero con la incorporación de la estructura de nodos CoordNode relacionados con listas enlazadas. CoordNode es un nodo en la lista enlazada que guarda el tipo y el valor del propio nodo, existiendo tres tipos de nodos: el nodo del jugador, el nodo izquierdo del Sensor y el nodo derecho del Sensor.
La mayor parte del trabajo de una lista ligada doble enlazada consiste en mantener la lista ordenada:
Cuando un jugador se une, se requiere mover el nodo del jugador a una posición ordenada, y al mismo tiempo que se mueve el nodo del jugador, manejar eventos de entrada o salida de otros jugadores en el área de interés alrededor del jugador.
Una vez que el jugador se haya desplazado a la posición correcta, los nodos izquierdo y derecho del Sensor se moverán desde la posición del jugador hacia adelante y hacia atrás, hasta llegar a la posición correcta, y gestionarán los eventos de entrada y salida que se produzcan al cruzar los nodos de otros jugadores.
Cuando el jugador se mueve, se actualiza la coordenada del jugador y se mueven los nodos del jugador y Sensor hacia la izquierda y derecha, gestionando la entrada y salida del área de interés.
El código del nodo móvil es el siguiente. Cada vez que se cruza un nodo, se llama a la función MoveCross. Esta función, según la dirección del movimiento y el tipo de nodo que se ha cruzado, decide si se entra o se sale del AOI.
void ListUpdateNode(CoordNode **list, CoordNode *pnode) {
float value = pnode->value;
if (pnode->next && pnode->next->value < value) {
// move right
auto cur_node = pnode->next;
while (1) {
MoveCross(MOVE_DIRECTION_RIGHT, pnode, cur_node);
if (!cur_node->next || cur_node->next->value >= value) break;
cur_node = cur_node->next;
}
ListRemove(list, pnode);
ListInsertAfter(list, cur_node, pnode);
} else if (pnode->prev && pnode->prev->value > value) {
// move left
auto cur_node = pnode->prev;
while (1) {
MoveCross(MOVE_DIRECTION_LEFT, pnode, cur_node);
if (!cur_node->prev || cur_node->prev->value <= value) break;
cur_node = cur_node->prev;
}
ListRemove(list, pnode);
ListInsertBefore(list, cur_node, pnode);
}
}
El movimiento en la lista enlazada es muy lento, con una complejidad de O(n), especialmente cuando un nuevo jugador se une a la escena, ya que debe moverse gradualmente desde una distancia infinita hasta la posición correcta, lo que requiere recorrer muchos nodos y consume bastante recursos. Para optimizar el rendimiento, podemos colocar faros en posiciones fijas dentro de la escena. Estos faros funcionan de manera similar a los jugadores, con la única diferencia de que registran una copia adicional de los datos detected_by, que se utiliza para identificar en qué rangos de Sensor se encuentra esa entidad centinela. Cuando un jugador entra por primera vez en la escena, ya no comienza a moverse desde la distancia más lejana, sino que encuentra un faro cercano, inserta el nodo junto a este faro y, gracias a los datos detected_by del faro, accede rápidamente al rango de AOI de otros jugadores que coinciden con el faro, y luego comienza a moverse hacia la posición correcta, teniendo en cuenta las entradas y salidas en el proceso. De manera similar, para los Sensor, se puede heredar primero los datos del faro y luego moverse desde la ubicación del faro hacia la posición correcta. Estas dos optimizaciones pueden mejorar el rendimiento de inserción de jugadores en más del doble.
Sensor tiene también un HashMap llamado aoi_player_candidates (aquí se utilizó khashLa AOI generada por el movimiento de nodos solo puede detectar un área cuadrada con un lado de "2r" en el eje X-Z, que no es estrictamente un área circular como se desea. Las entidades dentro de esta área cuadrada se registran en aoi_player_candidates y se recorren en el Tick para calcular el alcance de la AOI dentro del área circular, por lo tanto se denominan candidates.
Todas las operaciones de la lista de doble enlace cruzada están destinadas a mantener de manera constante las entidades candidates dentro de una región cuadrada. Las operaciones realizadas por Tick en la lista de doble enlace cruzada son prácticamente las mismas que en la cuadrícula, aunque la forma de recorrer y calcular los candidates de AOI es diferente. Los candidates de la cuadrícula son las entidades de las celdas que están cubiertas por la región circular de AOI, mientras que en la lista de doble enlace cruzada se define una región cuadrada de lado 2r delimitada por los nodos izquierdo y derecho del Sensor. En términos cualitativos, los candidates de la lista de doble enlace cruzada generalmente son menos que en la cuadrícula, por lo que el número de iteraciones en Tick es menor y su rendimiento es superior. Sin embargo, la lista de doble enlace cruzada también implica un gran consumo adicional de rendimiento para mantener la lista. En definitiva, vamos a realizar pruebas para ver cuál de los dos enfoques es más eficiente.
Rendimiento medido
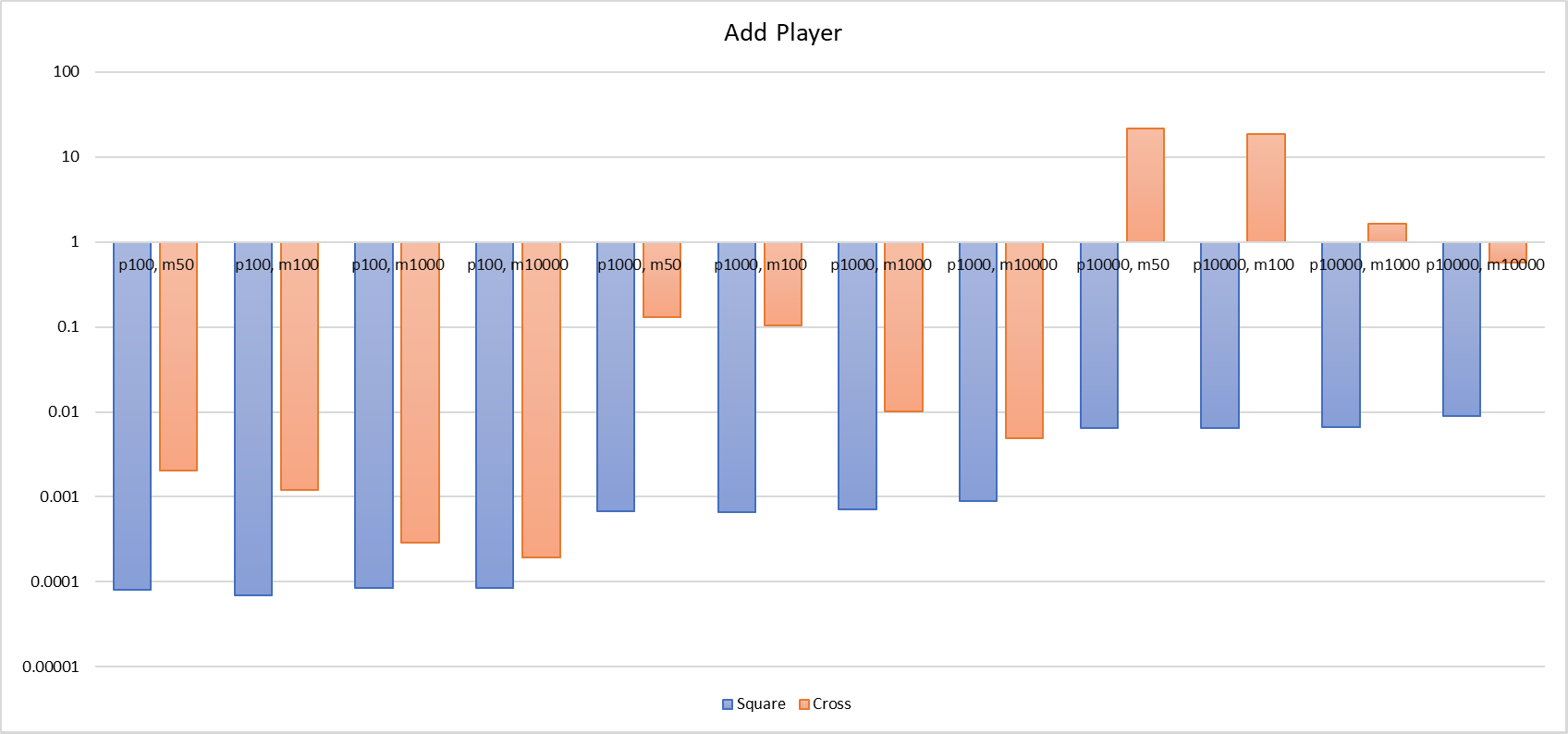
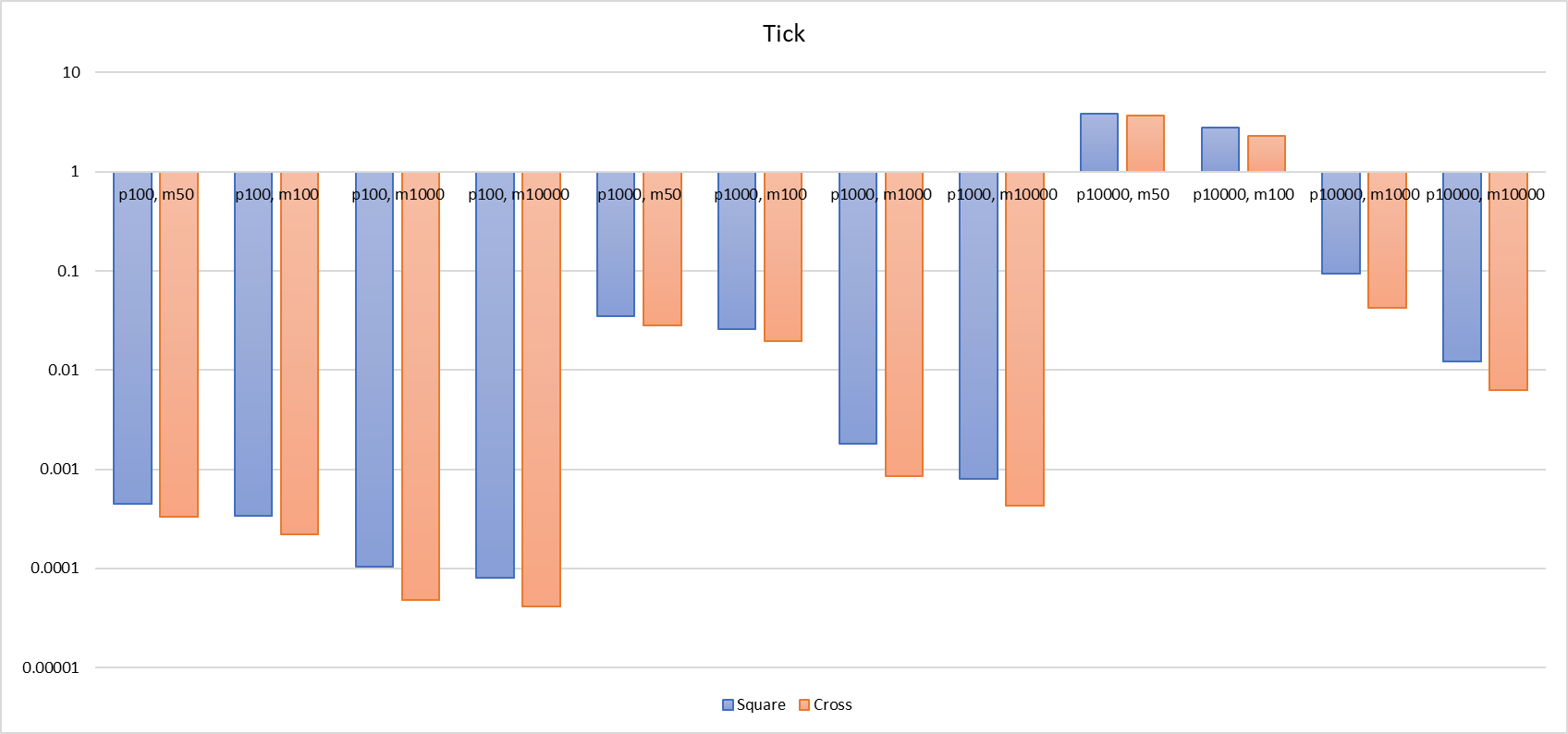
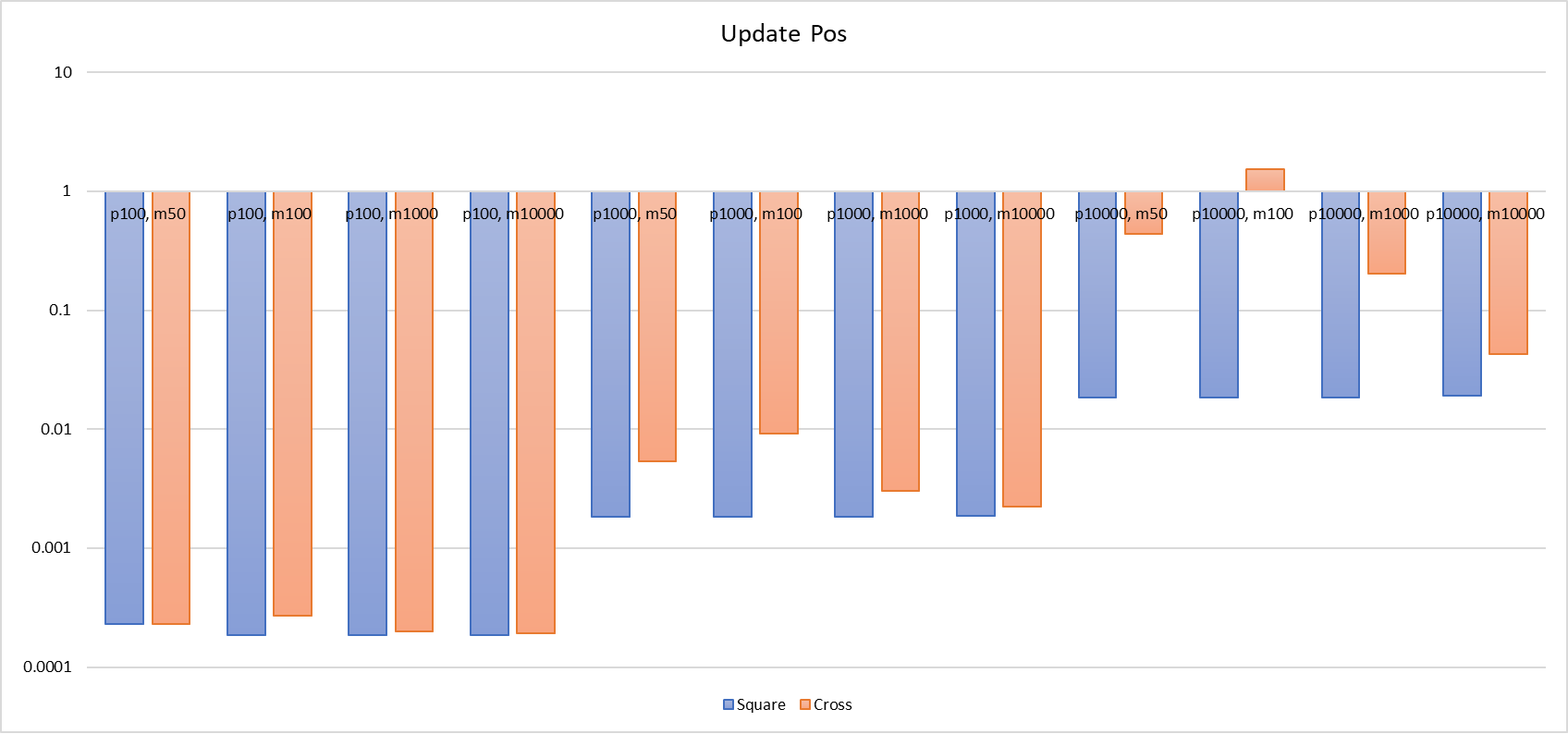
He medido el tiempo de consumo en tres situaciones: cuando el jugador se une a la escena (Add Player), el cálculo de eventos de entrada y salida del AOI (Tick), y la actualización de la posición del jugador (Update Pos).
Los jugadores son generados aleatoriamente dentro del rango del mapa y luego se incorporan a la escena. player_num se refiere a la cantidad de jugadores, y map_size es el rango de coordenadas X-Z del mapa. Las posiciones de los jugadores se generan de forma uniforme dentro de este rango, y cada jugador tiene un Sensor con un radio de 100 unidades que sirve como Área de Interés (AOI). Para medir el tiempo se utiliza boost::timer::cpu_timer. Se han considerado tres casos para player_num: 100, 1000, 10000, y cuatro casos para map_size: [-50, 50], [-100, 100], [-1000, 1000], [-10000, 10000].
Actualizar la posición del jugador hará que se mueva en una dirección aleatoria fija, a una velocidad de 6m/s.
El entorno de prueba está:
- CPU: Intel(R) Core(TM) i5-4590 CPU @ 3.30GHz Sistema: Debian GNU/Linux 10 (Buster)
- versión de gcc: gcc version 8.3.0 (Debian 8.3.0-6)
- versión de boost: boost_1_75_0
Prueba de cuadrícula de nueve posiciones.
Los resultados de la prueba de la matriz de 9 cuadros son los siguientes:
===Begin Milestore: player_num = 100, map_size = (-50.000000, 50.000000)
Add Player (1 times) 0.000081s wall, 0.000000s user + 0.000000s system = 0.000000s CPU (n/a%)
Tick (1 times) 0.000452s wall, 0.000000s user + 0.000000s system = 0.000000s CPU (n/a%)
Update Pos (10 times) 0.000230s wall, 0.000000s user + 0.000000s system = 0.000000s CPU (n/a%)
===End Milestore
===Begin Milestore: player_num = 100, map_size = (-100.000000, 100.000000)
Add Player (1 times) 0.000070s wall, 0.000000s user + 0.000000s system = 0.000000s CPU (n/a%)
Tick (1 times) 0.000338s wall, 0.000000s user + 0.000000s system = 0.000000s CPU (n/a%)
Update Pos (10 times) 0.000185s wall, 0.000000s user + 0.000000s system = 0.000000s CPU (n/a%)
===End Milestore
===Begin Milestore: player_num = 100, map_size = (-1000.000000, 1000.000000)
Add Player (1 times) 0.000084s wall, 0.000000s user + 0.000000s system = 0.000000s CPU (n/a%)
Tick (1 times) 0.000103s wall, 0.000000s user + 0.000000s system = 0.000000s CPU (n/a%)
Update Pos (10 times) 0.000187s wall, 0.000000s user + 0.000000s system = 0.000000s CPU (n/a%)
===End Milestore
===Begin Milestore: player_num = 100, map_size = (-10000.000000, 10000.000000)
Add Player (1 times) 0.000084s wall, 0.000000s user + 0.000000s system = 0.000000s CPU (n/a%)
Tick (1 times) 0.000080s wall, 0.000000s user + 0.000000s system = 0.000000s CPU (n/a%)
Update Pos (10 times) 0.000185s wall, 0.000000s user + 0.000000s system = 0.000000s CPU (n/a%)
===End Milestore
===Begin Milestore: player_num = 1000, map_size = (-50.000000, 50.000000)
Add Player (1 times) 0.000673s wall, 0.000000s user + 0.000000s system = 0.000000s CPU (n/a%)
Tick (1 times) 0.035298s wall, 0.030000s user + 0.000000s system = 0.030000s CPU (85.0%)
Update Pos (10 times) 0.001841s wall, 0.000000s user + 0.000000s system = 0.000000s CPU (n/a%)
===End Milestore
===Begin Milestore: player_num = 1000, map_size = (-100.000000, 100.000000)
Add Player (1 times) 0.000664s wall, 0.000000s user + 0.000000s system = 0.000000s CPU (n/a%)
Tick (1 times) 0.025806s wall, 0.030000s user + 0.000000s system = 0.030000s CPU (116.3%)
Update Pos (10 times) 0.001842s wall, 0.000000s user + 0.000000s system = 0.000000s CPU (n/a%)
===End Milestore
===Begin Milestore: player_num = 1000, map_size = (-1000.000000, 1000.000000)
Add Player (1 times) 0.000721s wall, 0.000000s user + 0.000000s system = 0.000000s CPU (n/a%)
Tick (1 times) 0.001793s wall, 0.000000s user + 0.000000s system = 0.000000s CPU (n/a%)
Update Pos (10 times) 0.001849s wall, 0.010000s user + 0.000000s system = 0.010000s CPU (540.8%)
===End Milestore
===Begin Milestore: player_num = 1000, map_size = (-10000.000000, 10000.000000)
Add Player (1 times) 0.000885s wall, 0.000000s user + 0.000000s system = 0.000000s CPU (n/a%)
Tick (1 times) 0.000804s wall, 0.000000s user + 0.000000s system = 0.000000s CPU (n/a%)
Update Pos (10 times) 0.001855s wall, 0.000000s user + 0.000000s system = 0.000000s CPU (n/a%)
===End Milestore
===Begin Milestore: player_num = 10000, map_size = (-50.000000, 50.000000)
Add Player (1 times) 0.006454s wall, 0.010000s user + 0.000000s system = 0.010000s CPU (154.9%)
Tick (1 times) 3.822028s wall, 3.800000s user + 0.020000s system = 3.820000s CPU (99.9%)
Update Pos (10 times) 0.018402s wall, 0.020000s user + 0.000000s system = 0.020000s CPU (108.7%)
===End Milestore
===Begin Milestore: player_num = 10000, map_size = (-100.000000, 100.000000)
Add Player (1 times) 0.006439s wall, 0.000000s user + 0.000000s system = 0.000000s CPU (n/a%)
Tick (1 times) 2.805551s wall, 2.760000s user + 0.040000s system = 2.800000s CPU (99.8%)
Update Pos (10 times) 0.018489s wall, 0.010000s user + 0.000000s system = 0.010000s CPU (54.1%)
===End Milestore
===Begin Milestore: player_num = 10000, map_size = (-1000.000000, 1000.000000)
Add Player (1 times) 0.006698s wall, 0.010000s user + 0.000000s system = 0.010000s CPU (149.3%)
Tick (1 times) 0.093759s wall, 0.100000s user + 0.000000s system = 0.100000s CPU (106.7%)
Update Pos (10 times) 0.018350s wall, 0.010000s user + 0.000000s system = 0.010000s CPU (54.5%)
===End Milestore
===Begin Milestore: player_num = 10000, map_size = (-10000.000000, 10000.000000)
Add Player (1 times) 0.009046s wall, 0.010000s user + 0.000000s system = 0.010000s CPU (110.6%)
Tick (1 times) 0.012091s wall, 0.010000s user + 0.000000s system = 0.010000s CPU (82.7%)
Update Pos (10 times) 0.019033s wall, 0.020000s user + 0.000000s system = 0.020000s CPU (105.1%)
===End Milestore
Cuando hay 100 jugadores en el tablero de nueve cuadrados, las tres operaciones son muy rápidas. En el caso extremo con un tamaño de mapa de [-50, 50], todos los jugadores están dentro del área de influencia (AOI por sus siglas en inglés) unos de otros y el tiempo de Tick es aproximadamente de 0.4ms. Tanto la adición de jugadores al escenario como la actualización de coordenadas tienen una complejidad lineal de O(número_de_jugadores), y el rendimiento es bueno. Cuando el número de jugadores llega a 10,000 en un mapa de [-50, 50], tanto la adición de jugadores como la actualización de posiciones se completan en unos pocos milisegundos debido a la linealidad, sin embargo, el tiempo de Tick aumenta a 3.8 segundos, lo que consume una gran cantidad de CPU y se vuelve inutilizable. Con 10,000 jugadores y un tamaño de mapa de [-1000, 1000], el tiempo de Tick aumenta a aproximadamente 94ms. Si se pudiera reducir la frecuencia de Tick, por ejemplo, a dos veces por segundo, todavía estaría dentro del rango de utilidad, aunque apenas.
Lista cruzada probada en la práctica.
Los resultados de las pruebas de la lista enlazada en cruz son los siguientes:
===Begin Milestore: player_num = 100, map_size = (-50.000000, 50.000000)
Add Player (1 times) 0.002057s wall, 0.000000s user + 0.000000s system = 0.000000s CPU (n/a%)
Tick (1 times) 0.000330s wall, 0.000000s user + 0.000000s system = 0.000000s CPU (n/a%)
Update Pos (10 times) 0.000232s wall, 0.000000s user + 0.000000s system = 0.000000s CPU (n/a%)
===End Milestore
===Begin Milestore: player_num = 100, map_size = (-100.000000, 100.000000)
Add Player (1 times) 0.001201s wall, 0.000000s user + 0.000000s system = 0.000000s CPU (n/a%)
Tick (1 times) 0.000222s wall, 0.000000s user + 0.000000s system = 0.000000s CPU (n/a%)
Update Pos (10 times) 0.000272s wall, 0.000000s user + 0.000000s system = 0.000000s CPU (n/a%)
===End Milestore
===Begin Milestore: player_num = 100, map_size = (-1000.000000, 1000.000000)
Add Player (1 times) 0.000288s wall, 0.000000s user + 0.000000s system = 0.000000s CPU (n/a%)
Tick (1 times) 0.000048s wall, 0.000000s user + 0.000000s system = 0.000000s CPU (n/a%)
Update Pos (10 times) 0.000200s wall, 0.000000s user + 0.000000s system = 0.000000s CPU (n/a%)
===End Milestore
===Begin Milestore: player_num = 100, map_size = (-10000.000000, 10000.000000)
Add Player (1 times) 0.000194s wall, 0.000000s user + 0.000000s system = 0.000000s CPU (n/a%)
Tick (1 times) 0.000041s wall, 0.000000s user + 0.000000s system = 0.000000s CPU (n/a%)
Update Pos (10 times) 0.000192s wall, 0.000000s user + 0.000000s system = 0.000000s CPU (n/a%)
===End Milestore
===Begin Milestore: player_num = 1000, map_size = (-50.000000, 50.000000)
Add Player (1 times) 0.130766s wall, 0.130000s user + 0.000000s system = 0.130000s CPU (99.4%)
Tick (1 times) 0.028091s wall, 0.020000s user + 0.000000s system = 0.020000s CPU (71.2%)
Update Pos (10 times) 0.005369s wall, 0.010000s user + 0.000000s system = 0.010000s CPU (186.2%)
===End Milestore
===Begin Milestore: player_num = 1000, map_size = (-100.000000, 100.000000)
Add Player (1 times) 0.103015s wall, 0.100000s user + 0.000000s system = 0.100000s CPU (97.1%)
Tick (1 times) 0.019545s wall, 0.020000s user + 0.000000s system = 0.020000s CPU (102.3%)
Update Pos (10 times) 0.009208s wall, 0.010000s user + 0.000000s system = 0.010000s CPU (108.6%)
===End Milestore
===Begin Milestore: player_num = 1000, map_size = (-1000.000000, 1000.000000)
Add Player (1 times) 0.010150s wall, 0.010000s user + 0.000000s system = 0.010000s CPU (98.5%)
Tick (1 times) 0.000845s wall, 0.000000s user + 0.000000s system = 0.000000s CPU (n/a%)
Update Pos (10 times) 0.003023s wall, 0.000000s user + 0.000000s system = 0.000000s CPU (n/a%)
===End Milestore
===Begin Milestore: player_num = 1000, map_size = (-10000.000000, 10000.000000)
Add Player (1 times) 0.004950s wall, 0.010000s user + 0.000000s system = 0.010000s CPU (202.0%)
Tick (1 times) 0.000427s wall, 0.000000s user + 0.000000s system = 0.000000s CPU (n/a%)
Update Pos (10 times) 0.002234s wall, 0.000000s user + 0.000000s system = 0.000000s CPU (n/a%)
===End Milestore
===Begin Milestore: player_num = 10000, map_size = (-50.000000, 50.000000)
Add Player (1 times) 21.606402s wall, 21.040000s user + 0.570000s system = 21.610000s CPU (100.0%)
Tick (1 times) 3.696885s wall, 3.680000s user + 0.030000s system = 3.710000s CPU (100.4%)
Update Pos (10 times) 0.434396s wall, 0.430000s user + 0.000000s system = 0.430000s CPU (99.0%)
===End Milestore
===Begin Milestore: player_num = 10000, map_size = (-100.000000, 100.000000)
Add Player (1 times) 18.499235s wall, 18.470000s user + 0.020000s system = 18.490000s CPU (100.0%)
Tick (1 times) 2.292608s wall, 2.290000s user + 0.000000s system = 2.290000s CPU (99.9%)
Update Pos (10 times) 1.522617s wall, 1.530000s user + 0.000000s system = 1.530000s CPU (100.5%)
===End Milestore
===Begin Milestore: player_num = 10000, map_size = (-1000.000000, 1000.000000)
Add Player (1 times) 1.642519s wall, 1.640000s user + 0.000000s system = 1.640000s CPU (99.8%)
Tick (1 times) 0.042767s wall, 0.050000s user + 0.000000s system = 0.050000s CPU (116.9%)
Update Pos (10 times) 0.202949s wall, 0.200000s user + 0.000000s system = 0.200000s CPU (98.5%)
===End Milestore
===Begin Milestore: player_num = 10000, map_size = (-10000.000000, 10000.000000)
Add Player (1 times) 0.571257s wall, 0.570000s user + 0.000000s system = 0.570000s CPU (99.8%)
Tick (1 times) 0.006325s wall, 0.010000s user + 0.000000s system = 0.010000s CPU (158.1%)
Update Pos (10 times) 0.042568s wall, 0.040000s user + 0.000000s system = 0.040000s CPU (94.0%)
===End Milestore
Como hemos analizado antes, la lista de enlace cruzado tarda más tiempo en las operaciones de "Agregar Jugador" y "Actualizar Posición", especialmente en "Agregar Jugador", donde el rendimiento es incluso cientos o miles de veces peor en comparación con la cuadrícula de nueve celdas. Por ejemplo, en una prueba con un total de 100 jugadores y un rango de coordenadas de [-50, 50], la lista de enlace cruzado tomó 2ms, mientras que la cuadrícula de nueve celdas solo tomó 0.08ms. En otra prueba con 10000 jugadores y el mismo rango de coordenadas, la lista de enlace cruzado tomó 21.6s, mientras que la cuadrícula de nueve celdas solo tomó 6ms. En cuanto a la operación de "Actualizar Posición", también hay una diferencia considerable, con la lista de enlace cruzado tardando hasta cien veces más que la cuadrícula de nueve celdas. En una prueba con 10000 jugadores y un rango de coordenadas de [-100, 100], la lista de enlace cruzado tardó 1.5s para actualizar las posiciones de los jugadores, mientras que la cuadrícula de nueve celdas solo tomó 18ms. Se puede observar que la lista de enlace cruzado tiene un rango límite de tiempo más amplio en las operaciones de "Agregar Jugador" y "Actualizar Posición" en comparación con la cuadrícula de nueve celdas. Además, está más influenciada por el número de jugadores y el tamaño del mapa. En áreas con una alta densidad de jugadores, el rendimiento de estas dos operaciones disminuirá rápidamente hasta volverse inutilizables.
En comparación con la operación Tick de la cadena cruzada, el rendimiento general es efectivamente mejor que el de la cuadrícula. En el mejor de los casos, el tiempo de ejecución es aproximadamente la mitad del de la cuadrícula (1000, [-1000, 1000] bajo la cadena cruzada toma 0.8ms, mientras que la cuadrícula toma 1.8ms); sin embargo, en el peor de los casos, la cadena cruzada puede degradarse a un rendimiento similar al de la cuadrícula (10000, [-10000, 10000] bajo la cadena cruzada toma 3.7s, la cuadrícula 3.8s). Esto se debe a que, en escenarios pequeños, los jugadores están mutuamente dentro del rango AOI, y la cantidad de candidatos que la cadena cruzada recorre en su Tick es en realidad bastante similar a la de la cuadrícula.
Para que la cadena cruzada funcione mejor que el cuadrado mágico, se necesitan algunas suposiciones más fuertes, como player_num = 1000, map_size = [-1000, 1000]. En este caso, el tiempo de Tick para la cadena cruzada es de 0.8ms, mientras que el del cuadrado mágico es de 1.8ms. Para Update Pos, la cadena cruzada toma 0.3ms y el cuadrado mágico 0.18ms (ten en cuenta que el tiempo de prueba de Update Pos es la suma total del tiempo de 10 ejecuciones). En el tiempo total de Tick + Update Pos, para que la cadena cruzada sea más eficiente que el cuadrado mágico, el número de Update Pos no debe superar 8 veces el de Tick, o dicho de otra manera, entre dos Tick, el número de Update Pos debe ser menor que 8. Además, dado que el tiempo de Add Player en la cadena cruzada es considerablemente alto, no es adecuada para situaciones en las que los jugadores entran y salen del escenario con frecuencia en un corto periodo de tiempo, o para teletransportes de gran alcance dentro del escenario. Asimismo, si un gran número de jugadores entra en el escenario en un breve lapso de tiempo, también puede provocar una disminución en el rendimiento y un alto consumo de CPU.
En cuanto a la lista de cruz, se puede optimizar eliminando el Tick, siempre y cuando el juego pueda aceptar un AOI cuadrado y se pueda tolerar el aumento de consumo en aspectos como la red derivado del AOI cuadrado en las pruebas. La premisa es bastante estricta, ya que en los juegos el CPU utilizado para el cálculo del AOI suele ser relativamente bajo, pero al cambiar de un AOI circular a uno cuadrado, el área del AOI aumenta y, por lo tanto, el número de jugadores en el área también aumenta, pudiendo llegar a ser un 1.27 veces mayor con una distribución uniforme de jugadores. No obstante, si se cumplen estas condiciones, la lista de cruz podría prescindir de la necesidad del Tick para actualizar regularmente los eventos del AOI, ya que el mantenimiento de la lista de candidatos de la lista de cruz bajo un AOI cuadrado permitiría evitar recorrer nuevamente en el Tick para calcular distancias, como se hacía anteriormente para el AOI circular. En este escenario, la lista de cruz podría lograr un rendimiento considerable, ya que la actualización de la posición en la lista de cruz podría ser varias veces o incluso decenas de veces más eficiente que el Tick.
Finalmente, se presenta un gráfico de barras comparativo entre ambos.
Resumen
Este texto presenta los principios y la implementación básica de dos algoritmos AOI (cuadrícula de nueve y cadena de cruz), analizando el rendimiento de ambos algoritmos a través de datos medidos. Se espera que esto pueda ser útil o inspirador para los lectores.
En general, el método de la cuadrícula de 9 celdas es fácil de implementar, equilibrado en rendimiento y no suele presentar problemas. Es muy adecuado para juegos donde la AOI no es un cuello de botella. La variación de rendimiento del método de la cuadrícula de 9 celdas se mantiene dentro de un rango previsible, con un rendimiento mínimo relativamente alto y menos propenso a generar cuellos de botella. Por otro lado, el espacio de optimización no es tan grande y la complejidad temporal es más estable.
Por otro lado, el método de la cadena cruzada, aunque su implementación es más compleja y tiene un rendimiento mínimo inferior al del método de la cuadrícula de 9 celdas, si se cumplen ciertas suposiciones y condiciones previas, la cadena cruzada puede tener un mayor potencial de optimización en términos de espacio, es decir, su potencial máximo puede ser más alto. Ambos métodos tienen sus ventajas y desventajas, y en la industria de juegos, se elige uno u otro dependiendo de las necesidades específicas. Al final, la decisión dependerá de cada caso en particular.
Mis habilidades son limitadas, el contenido de este texto solo refleja mis pensamientos. Si hay alguna insuficiencia o inexactitud, agradezco los comentarios y la discusión.
Original: https://wiki.disenone.site/es
This post is protected by CC BY-NC-SA 4.0 agreement, should be reproduced with attribution.
Visitors. Total Visits. Page Visits.
Este mensaje ha sido traducido utilizando ChatGPT, por favor, en caso de 反馈Indique cualquier omisión.