Analyse et test de performance de l'algorithme AOI de jeu.
Introduction
"AOI" (Area Of Interest) is a fundamental feature in multiplayer online games, where players need to receive information about other players or entities (Entities) entering their field of view. The algorithms that determine which entities are within a player's field of view and which ones enter or leave it are commonly referred to as AOI algorithms.
Ce texte discute de deux algorithmes AOI : le carré magique et la croix, et donne une analyse de performance expérimentale des deux algorithmes pour que vous puissiez les utiliser en toute confiance et ne pas paniquer face aux problèmes.
Le texte mentionnera deux termes : "joueur" et "entité". Une entité est une notion d'objet dans le jeu, tandis qu'un joueur est une entité ayant une zone d'intérêt (AOI).
Le code mentionné dans le texte peut être trouvé ici : AoiTesting.
Carré magique
Le concept de grille en neuf parties consiste à diviser les positions de toutes les entités dans un scénario en cases, en les regroupant par exemple en carrés de 200 unités de côté. Pour repérer les autres entités à l'intérieur de la zone d'intérêt de AOI, il faut comparer tous les joueurs présents dans les cases incluses dans cette zone.
Par exemple, la scène tick toutes les 100 millisecondes, et dans chaque tick, nous pouvons mettre à jour l'AOI du joueur de cette manière :
- Ensemble de cases impliquées dans le calcul du rayon AOI centré sur la position du joueur
- Calculer la distance de chaque entité dans l'ensemble de grilles par rapport au joueur.
- L'ensemble des entités dont la distance est inférieure au rayon de l'AOI constitue le nouvel AOI du joueur.
Le "Nine-Grid Algorithm" est assez simple à mettre en œuvre, il peut être décrit en quelques phrases. Nous garderons l'analyse de performance spécifique pour plus tard, commençons par examiner l'algorithme de "Cross-List".
Liste doublement chaînée
Pour les jeux en 3D, nous avons tendance à construire des listes chaînées ordonnées séparées pour les coordonnées X et Z. Chaque entité du jeu possède un nœud dans ces listes contenant sa valeur sur l'axe correspondant, classé par ordre croissant. Cependant, si nous stockons uniquement les points de coordonnées des entités, l'efficacité de recherche reste toujours faible pour ces deux listes.
Ce qui est vraiment crucial, c'est qu'on ajoute à chaque joueur qui possède l'AOI deux nœuds sentinelles de chaque côté de la liste chaînée. Les coordonnées des deux sentinelles diffèrent exactement du rayon de l'AOI par rapport aux coordonnées du joueur lui-même. Par exemple, si les coordonnées du joueur P sont (a, b, c), et que le rayon de l'AOI est r, il y aura deux sentinelles sur l'axe des X, left_x et right_x, avec des coordonnées respectives de a - r et a + r. En raison de la présence des sentinelles, nous mettons à jour l'AOI en suivant les déplacements des sentinelles par rapport aux autres nœuds entités. Prenons l'exemple précédent, si une entité E se déplace de manière à traverser de droite à gauche la sentinelle left_x, c'est-à-dire en passant de la droite de left_x à la gauche de left_x, alors cela signifie que E a certainement quitté l'AOI de P; de même, si elle traverse right_x de droite à gauche, elle a quitté l'AOI. En revanche, si elle traverse left_x de droite à gauche ou right_x de gauche à droite, cela signifie qu'il est possible qu'elle entre dans l'AOI de P.
On peut observer que l'algorithme de liste en croix est beaucoup plus complexe que la grille en neuf cases. Il faut maintenir deux listes ordonnées, synchroniser le déplacement des nœuds des listes à chaque mise à jour des coordonnées entités, et mettre à jour la zone d'intérêt des objets lors du déplacement au-dessus des autres nœuds.
La réalisation du carré magique
Parce qu'il s'agit de performances mesurées, examinons d'abord plus en détail les aspects de l'implémentation de l'algorithme du carré magique :
struct Sensor {
// ...
Nuid sensor_id;
float radius;
float radius_square;
PlayerPtrList aoi_players[2];
};
struct PlayerAoi {
// ...
Nuid nuid;
SquareId square_id;
int square_index;
Pos pos;
Pos last_pos;
Uint32 flags;
std::vector<Sensor> sensors;
};
Le PlayerAoi stocke les données des joueurs, comprenant un tableau sensors utilisé pour calculer les entités dans une certaine plage. Après chaque Tick, les entités calculées sont placées dans aoi_players. aoi_players contient deux tableaux pour comparer les résultats entre deux Ticks successifs, permettant de déterminer les entrées et sorties des joueurs. Le processus approximatif du Tick est le suivant:
AoiUpdateInfos SquareAoi::Tick() {
AoiUpdateInfos update_infos;
PlayerPtrList remove_list;
for (auto& elem : player_map_) {
auto& player = *elem.second;
// ...
// Calculer Aoi pour les joueurs avec des capteurs
if (!player.sensors.empty()) {
auto update_info = _UpdatePlayerAoi(cur_aoi_map_idx_, &player);
if (!update_info.sensor_update_list.empty()) {
update_infos.emplace(update_info.nuid, std::move(update_info));
}
}
// ...
}
// ...
// Enregistrer la dernière position du joueur
for (auto& elem : player_map_) {
auto& player = *elem.second;
player.last_pos = player.pos;
}
cur_aoi_map_idx_ = 1 - cur_aoi_map_idx_;
return update_infos;
}
Les actions effectuées par la fonction Tick sont simples : elle parcourt les joueurs ayant des capteurs, calcule un par un les entités se trouvant dans la portée du capteur (c'est-à-dire dans sa zone d'intérêt, ou AOI). last_pos est utilisé pour déterminer si une entité est entrée dans la zone d'intérêt (AOI) ou en est sortie. Voici le code de la fonction _UpdatePlayerAoi :
AoiUpdateInfo SquareAoi::_UpdatePlayerAoi(Uint32 cur_aoi_map_idx, PlayerAoi* pptr) {
AoiUpdateInfo aoi_update_info;
aoi_update_info.nuid = pptr->nuid;
Uint32 new_aoi_map_idx = 1 - cur_aoi_map_idx;
for (auto& sensor : pptr->sensors) {
auto& old_aoi = sensor.aoi_players[cur_aoi_map_idx];
auto& new_aoi = sensor.aoi_players[new_aoi_map_idx];
(this->*calc_aoi_players_func_)(*pptr, sensor, &new_aoi);
SensorUpdateInfo update_info;
auto& enters = update_info.enters;
auto& leaves = update_info.leaves;
float radius_square = sensor.radius_square;
_CheckLeave(pptr, radius_square, old_aoi, &leaves);
_CheckEnter(pptr, radius_square, new_aoi, &enters);
if (enters.empty() && leaves.empty()) {
continue;
}
update_info.sensor_id = sensor.sensor_id;
aoi_update_info.sensor_update_list.push_back(std::move(update_info));
}
return aoi_update_info;
}
old_aoi est l'AOI calculé lors du dernier Tick, tandis que new_aoi est l'AOI à calculer pour ce Tick. new_aoi est déterminé en parcourant les entités de toutes les cellules dans la plage de l'AOI, en sélectionnant celles qui sont à une distance du joueur inférieure au rayon de l'AOI. Ensuite, avec les fonctions _CheckLeave et _CheckEnter, nous calculons les entités qui sortent et qui entrent dans l'AOI pour ce Tick. Par exemple, si l'entité last_pos de new_aoi n'est pas dans la portée de l'AOI, cela signifie que cette entité est entrée dans la zone de l'AOI lors de ce Tick. Le code détaillé peut être consulté dans le fichier source, nous n'en discuterons pas davantage ici.
Implémentation de la liste chaînée croisée
Par rapport à la grille de Sudoku, la mise en œuvre de la liste croisée est plus complexe. Commençons par examiner la structure de données de base :
struct CoordNode {
// ...
Uint8 type;
float value;
CoordNode *prev = nullptr;
CoordNode *next = nullptr;
PlayerAoi *pplayer;
Sensor *psensor;
};
KHASH_MAP_INIT_INT64(SensorHashMap, PlayerAoi*);
struct Sensor {
// ...
Nuid sensor_id;
float radius;
float radius_square;
PlayerAoi *pplayer;
CoordNode left_x;
CoordNode right_x;
CoordNode left_z;
CoordNode right_z;
PlayerPtrList aoi_players[2];
std::shared_ptr<khash_t(SensorHashMap)> aoi_player_candidates;
};
struct PlayerAoi {
// ...
Nuid nuid;
Pos pos;
Pos last_pos;
Uint32 flags;
CoordNode node_x;
CoordNode node_z;
std::vector<Sensor> sensors;
std::shared_ptr<boost::unordered_map<Nuid, std::vector<Nuid>>> detected_by;
};
Les termes Sensor et PlayerAoi sont en partie similaires au Carré de Lo Shu, mais incluent une structure de noeud de liste chaînée supplémentaire appelée CoordNode. CoordNode est un noeud sur la liste chaînée, il enregistre le type et la valeur du noeud lui-même, il existe trois types de noeuds : nœud joueur, nœud Sensor à gauche, nœud Sensor à droite.
La majeure partie du travail d'une liste chaînée est de maintenir la liste ordonnée :
- Lorsqu'un joueur rejoint, il doit déplacer son nœud de joueur à une position ordonnée, tout en gérant les événements d'entrée ou de sortie des zones d'intérêt (AOI) des autres joueurs pendant ce déplacement.
- Une fois que le joueur s'est déplacé vers la bonne position, les nœuds
Sensorse déplacent de l'avant vers l'arrière du joueur vers la bonne position, et gèrent les événements d'entrée et de sortie déclenchés en traversant les nœuds d'autres joueurs. Lorsque le joueur se déplace, mettez à jour les coordonnées du joueur, déplacez le nœud du joueur et les nœuds gauche et droit du capteur, et gérez l'entrée et la sortie de l'AOI.
Le code du nœud mobile est comme suit : chaque fois qu'un nœud est traversé, la fonction MoveCross est appelée. Celle-ci détermine, en fonction de la direction du mouvement et du type de nœud traversé, s'il faut entrer ou sortir de l'AOI.
void ListUpdateNode(CoordNode **list, CoordNode *pnode) {
float value = pnode->value;
if (pnode->next && pnode->next->value < value) {
// move right
auto cur_node = pnode->next;
while (1) {
MoveCross(MOVE_DIRECTION_RIGHT, pnode, cur_node);
if (!cur_node->next || cur_node->next->value >= value) break;
cur_node = cur_node->next;
}
ListRemove(list, pnode);
ListInsertAfter(list, cur_node, pnode);
} else if (pnode->prev && pnode->prev->value > value) {
// move left
auto cur_node = pnode->prev;
while (1) {
MoveCross(MOVE_DIRECTION_LEFT, pnode, cur_node);
if (!cur_node->prev || cur_node->prev->value <= value) break;
cur_node = cur_node->prev;
}
ListRemove(list, pnode);
ListInsertBefore(list, cur_node, pnode);
}
}
Le déplacement des listes chaînées est très lent, avec une complexité de O(n), surtout lorsque de nouveaux joueurs entrent dans la scène. Les joueurs doivent se déplacer progressivement depuis un point très éloigné jusqu'à la position correcte, ce qui nécessite une grande quantité de nœuds à parcourir, entraînant une forte consommation. Pour optimiser les performances, nous pouvons placer des phares à des emplacements fixes dans la scène. Ces phares fonctionnent de manière similaire aux joueurs, mais ils enregistrent un ensemble supplémentaire de données appelé detected_by, indiquant dans quels champs de capteurs l'entité sentinelle se trouve. Lorsqu'un joueur entre dans la scène pour la première fois, il ne commence plus son déplacement depuis le point le plus éloigné, mais recherche le phare le plus proche. En insérant le nœud à côté du phare et en utilisant les données detected_by du phare, le joueur peut rapidement entrer dans la zone AOI des autres joueurs correspondant au phare, puis se déplacer vers la position correcte. Bien sûr, lors du déplacement, il est également nécessaire de gérer les entrées et les sorties. De même, pour les capteurs, il est possible d'hériter d'abord des données du phare, puis de se déplacer depuis la position du phare vers la position correcte. Ces deux optimisations peuvent plus que doubler les performances d'insertion des joueurs.
Sensor comporte également un HashMap nommé aoi_player_candidates (ici, pour des raisons de performance, khashL'événement AOI déclenché par le déplacement du nœud ne peut en réalité détecter qu'une zone carrée de longueur de côté 2r sur les axes X-Z, ce n'est pas vraiment une zone AOI circulaire au sens strict. Les entités à l'intérieur de cette zone carrée sont enregistrées dans aoi_player_candidates et sont parcourues dans Tick pour calculer la portée de l'AOI dans la zone circulaire, d'où le terme candidats.
Toutes les opérations sur les listes croisées sont menées pour maintenir en permanence les entités 'candidats' à l'intérieur de la région carrée. Les opérations effectuées par la liste croisée Tick sont presque identiques à celles de la grille 3x3, à la différence que le calcul et la traversée des candidats de la zone AOI diffèrent. Les candidats de la grille 3x3 sont les entités couvertes par la région circulaire AOI, tandis que la liste croisée est définie par les nœuds gauche et droit du capteur délimitant des entités dans la région carrée de côté 2r. En termes qualitatifs, en général, les candidats de la liste croisée sont moins nombreux que ceux de la grille 3x3, ce qui se traduit par moins de traversées et des performances supérieures dans Tick. Cependant, la liste croisée impose également une charge de performance supplémentaire importante pour la maintenance de la liste. Il reste à déterminer quelle solution offre les meilleures performances dans l'ensemble, ce que nous vérifierons prochainement par des tests pratiques.
Performances mesurées
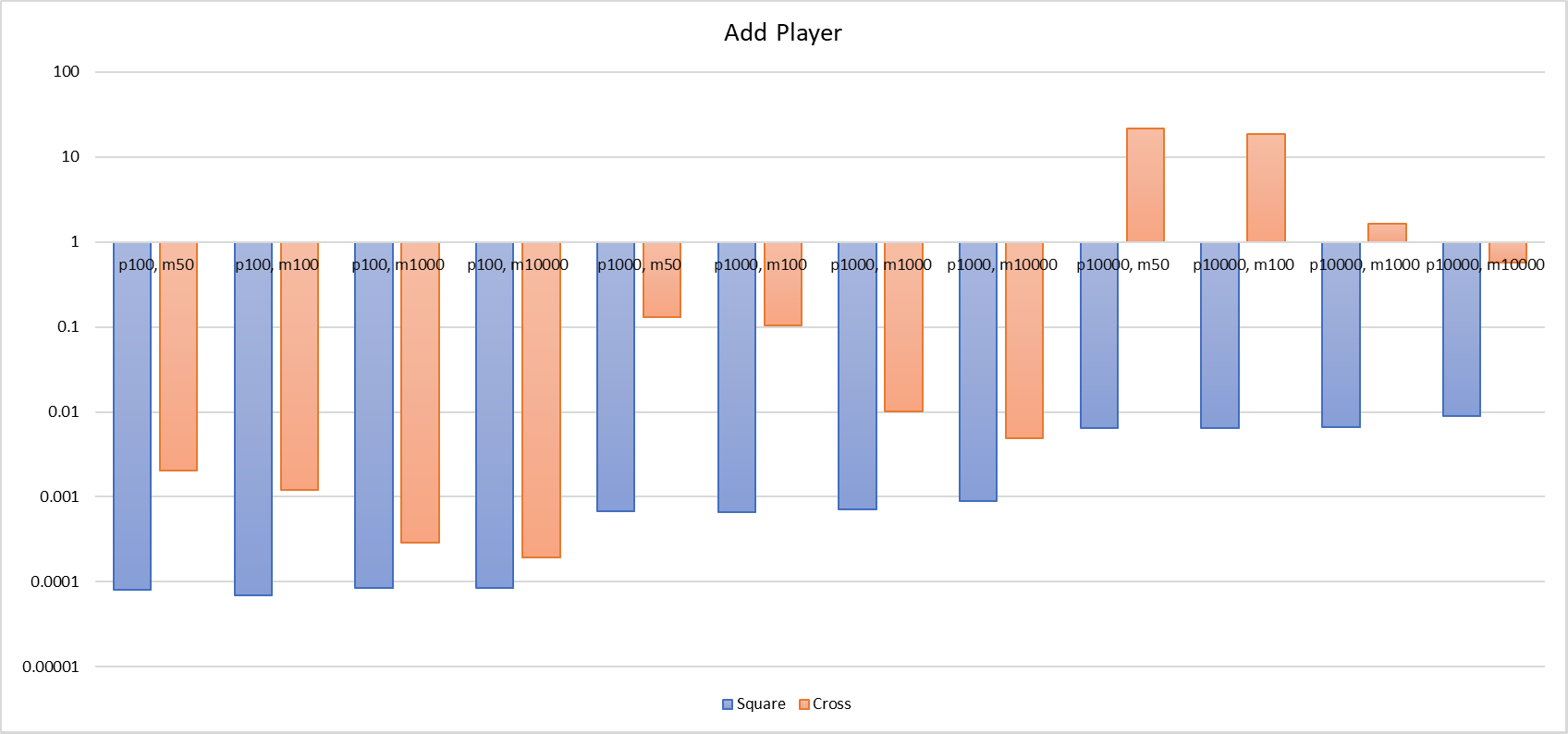
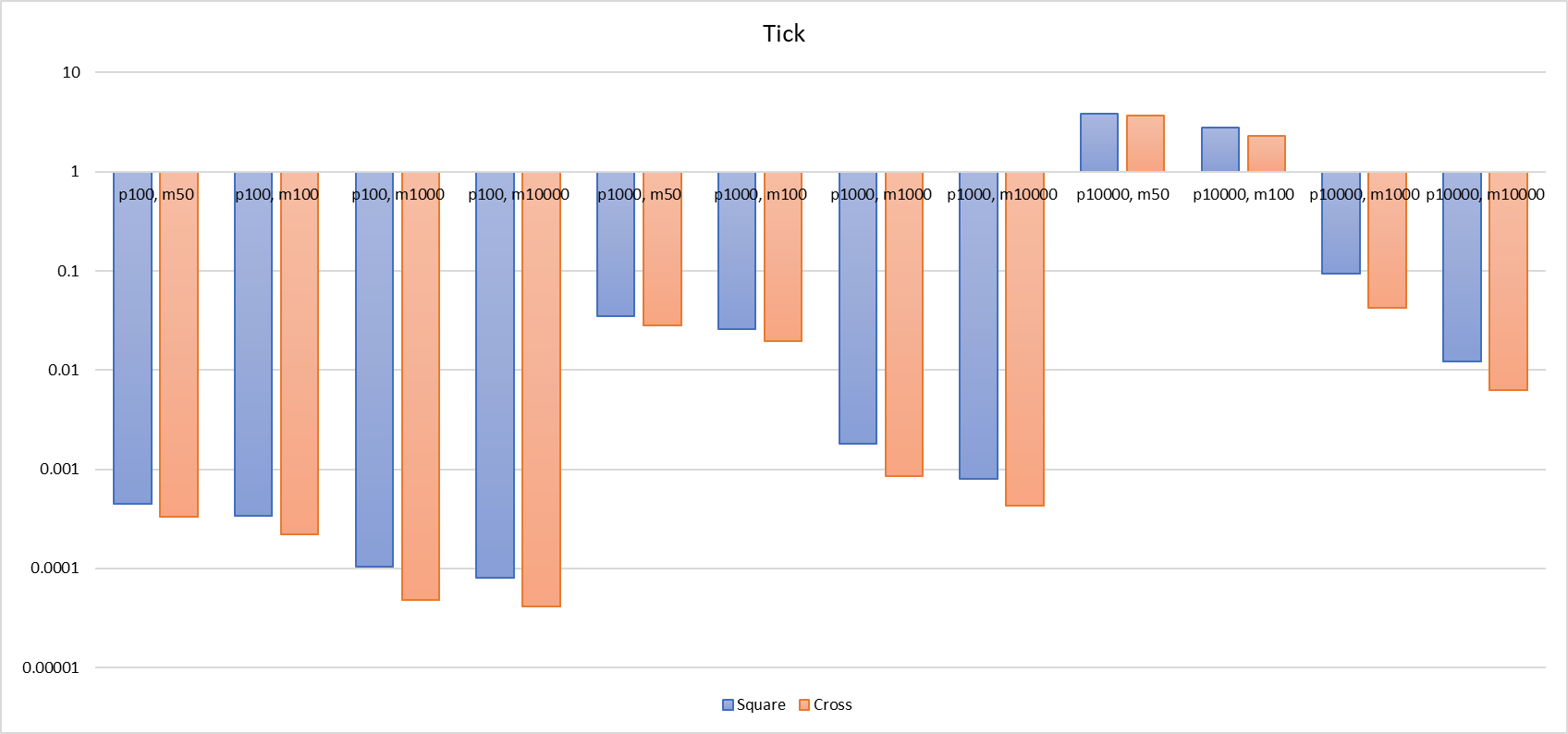
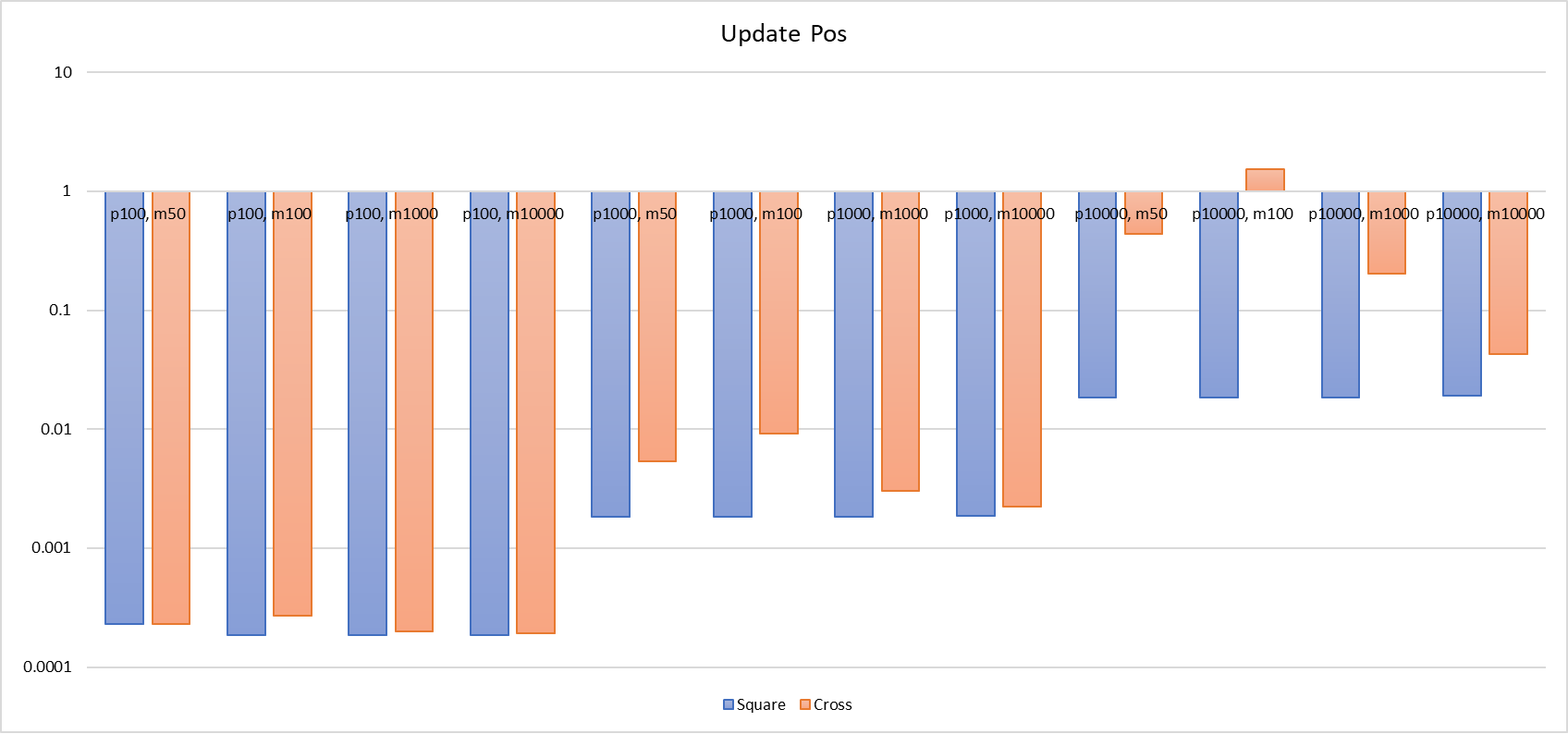
J'ai mesuré séparément le temps nécessaire pour que le joueur entre dans la scène (Add Player), pour traiter les événements d'entrée et de sortie de la zone d'intérêt (AOI) (Tick), et pour mettre à jour la position du joueur (Update Pos).
Les joueurs sont générés aléatoirement dans la plage de la carte, puis ajoutés à la scène. player_num désigne le nombre de joueurs, map_size est la plage des coordonnées X-Z de la carte. Les positions des joueurs sont générées uniformément dans cette plage, et chaque joueur a un capteur de rayon de 100 en tant que AOI. Le temps de calcul utilise boost::timer::cpu_timer. Trois cas ont été choisis pour player_num : 100, 1000, 10000, et quatre cas pour map_size : [-50, 50], [-100, 100], [-1000, 1000], [-10000, 10000].
Mettre à jour la position du joueur fixera le joueur dans une direction aléatoire, se déplaçant à une vitesse de 6m/s.
L'environnement de test pour cette fois est :
- CPU: Intel(R) Core(TM) i5-4590 CPU @ 3.30GHz Système : Debian GNU/Linux 10 (buster) Version de gcc : gcc version 8.3.0 (Debian 8.3.0-6) Version de boost : boost_1_75_0
Test réel de la grille à neuf cases
Les résultats du test du carré magique sont les suivants :
===Begin Milestore: player_num = 100, map_size = (-50.000000, 50.000000)
Add Player (1 times) 0.000081s wall, 0.000000s user + 0.000000s system = 0.000000s CPU (n/a%)
Tick (1 times) 0.000452s wall, 0.000000s user + 0.000000s system = 0.000000s CPU (n/a%)
Update Pos (10 times) 0.000230s wall, 0.000000s user + 0.000000s system = 0.000000s CPU (n/a%)
===End Milestore
===Begin Milestore: player_num = 100, map_size = (-100.000000, 100.000000)
Add Player (1 times) 0.000070s wall, 0.000000s user + 0.000000s system = 0.000000s CPU (n/a%)
Tick (1 times) 0.000338s wall, 0.000000s user + 0.000000s system = 0.000000s CPU (n/a%)
Update Pos (10 times) 0.000185s wall, 0.000000s user + 0.000000s system = 0.000000s CPU (n/a%)
===End Milestore
===Begin Milestore: player_num = 100, map_size = (-1000.000000, 1000.000000)
Add Player (1 times) 0.000084s wall, 0.000000s user + 0.000000s system = 0.000000s CPU (n/a%)
Tick (1 times) 0.000103s wall, 0.000000s user + 0.000000s system = 0.000000s CPU (n/a%)
Update Pos (10 times) 0.000187s wall, 0.000000s user + 0.000000s system = 0.000000s CPU (n/a%)
===End Milestore
===Begin Milestore: player_num = 100, map_size = (-10000.000000, 10000.000000)
Add Player (1 times) 0.000084s wall, 0.000000s user + 0.000000s system = 0.000000s CPU (n/a%)
Tick (1 times) 0.000080s wall, 0.000000s user + 0.000000s system = 0.000000s CPU (n/a%)
Update Pos (10 times) 0.000185s wall, 0.000000s user + 0.000000s system = 0.000000s CPU (n/a%)
===End Milestore
===Begin Milestore: player_num = 1000, map_size = (-50.000000, 50.000000)
Add Player (1 times) 0.000673s wall, 0.000000s user + 0.000000s system = 0.000000s CPU (n/a%)
Tick (1 times) 0.035298s wall, 0.030000s user + 0.000000s system = 0.030000s CPU (85.0%)
Update Pos (10 times) 0.001841s wall, 0.000000s user + 0.000000s system = 0.000000s CPU (n/a%)
===End Milestore
===Begin Milestore: player_num = 1000, map_size = (-100.000000, 100.000000)
Add Player (1 times) 0.000664s wall, 0.000000s user + 0.000000s system = 0.000000s CPU (n/a%)
Tick (1 times) 0.025806s wall, 0.030000s user + 0.000000s system = 0.030000s CPU (116.3%)
Update Pos (10 times) 0.001842s wall, 0.000000s user + 0.000000s system = 0.000000s CPU (n/a%)
===End Milestore
===Begin Milestore: player_num = 1000, map_size = (-1000.000000, 1000.000000)
Add Player (1 times) 0.000721s wall, 0.000000s user + 0.000000s system = 0.000000s CPU (n/a%)
Tick (1 times) 0.001793s wall, 0.000000s user + 0.000000s system = 0.000000s CPU (n/a%)
Update Pos (10 times) 0.001849s wall, 0.010000s user + 0.000000s system = 0.010000s CPU (540.8%)
===End Milestore
===Begin Milestore: player_num = 1000, map_size = (-10000.000000, 10000.000000)
Add Player (1 times) 0.000885s wall, 0.000000s user + 0.000000s system = 0.000000s CPU (n/a%)
Tick (1 times) 0.000804s wall, 0.000000s user + 0.000000s system = 0.000000s CPU (n/a%)
Update Pos (10 times) 0.001855s wall, 0.000000s user + 0.000000s system = 0.000000s CPU (n/a%)
===End Milestore
===Begin Milestore: player_num = 10000, map_size = (-50.000000, 50.000000)
Add Player (1 times) 0.006454s wall, 0.010000s user + 0.000000s system = 0.010000s CPU (154.9%)
Tick (1 times) 3.822028s wall, 3.800000s user + 0.020000s system = 3.820000s CPU (99.9%)
Update Pos (10 times) 0.018402s wall, 0.020000s user + 0.000000s system = 0.020000s CPU (108.7%)
===End Milestore
===Begin Milestore: player_num = 10000, map_size = (-100.000000, 100.000000)
Add Player (1 times) 0.006439s wall, 0.000000s user + 0.000000s system = 0.000000s CPU (n/a%)
Tick (1 times) 2.805551s wall, 2.760000s user + 0.040000s system = 2.800000s CPU (99.8%)
Update Pos (10 times) 0.018489s wall, 0.010000s user + 0.000000s system = 0.010000s CPU (54.1%)
===End Milestore
===Begin Milestore: player_num = 10000, map_size = (-1000.000000, 1000.000000)
Add Player (1 times) 0.006698s wall, 0.010000s user + 0.000000s system = 0.010000s CPU (149.3%)
Tick (1 times) 0.093759s wall, 0.100000s user + 0.000000s system = 0.100000s CPU (106.7%)
Update Pos (10 times) 0.018350s wall, 0.010000s user + 0.000000s system = 0.010000s CPU (54.5%)
===End Milestore
===Begin Milestore: player_num = 10000, map_size = (-10000.000000, 10000.000000)
Add Player (1 times) 0.009046s wall, 0.010000s user + 0.000000s system = 0.010000s CPU (110.6%)
Tick (1 times) 0.012091s wall, 0.010000s user + 0.000000s system = 0.010000s CPU (82.7%)
Update Pos (10 times) 0.019033s wall, 0.020000s user + 0.000000s system = 0.020000s CPU (105.1%)
===End Milestore
Lorsque le nombre de joueurs est de 100 dans la grille 9x9, les trois opérations sont très rapides, même dans des conditions extrêmes avec map_size = [-50, 50]. Tous les joueurs sont à portée AOI les uns des autres, et chaque Tick prend environ 0.4ms. L'ajout de joueurs et la mise à jour des coordonnées sont tous deux de complexité linéaire O(nbre_joueurs), avec de bonnes performances. Lorsque le nombre de joueurs atteint 10 000 avec map_size = [-50, 50], l'ajout de joueur et la mise à jour des positions prennent quelques millisecondes seulement, mais chaque Tick prend 3.8 secondes, nécessitant beaucoup de puissance CPU, ce qui le rend inutilisable. Avec 10 000 joueurs et une carte de taille [-1000, 1000], chaque Tick prend environ 94ms. Si la fréquence de Tick peut être réduite, par exemple à deux fois par seconde, cela reste tout juste dans une plage d'utilisation acceptable.
Liste croisée testée en pratique
Les résultats des tests de la liste chaînée croisée sont les suivants :
===Begin Milestore: player_num = 100, map_size = (-50.000000, 50.000000)
Add Player (1 times) 0.002057s wall, 0.000000s user + 0.000000s system = 0.000000s CPU (n/a%)
Tick (1 times) 0.000330s wall, 0.000000s user + 0.000000s system = 0.000000s CPU (n/a%)
Update Pos (10 times) 0.000232s wall, 0.000000s user + 0.000000s system = 0.000000s CPU (n/a%)
===End Milestore
===Begin Milestore: player_num = 100, map_size = (-100.000000, 100.000000)
Add Player (1 times) 0.001201s wall, 0.000000s user + 0.000000s system = 0.000000s CPU (n/a%)
Tick (1 times) 0.000222s wall, 0.000000s user + 0.000000s system = 0.000000s CPU (n/a%)
Update Pos (10 times) 0.000272s wall, 0.000000s user + 0.000000s system = 0.000000s CPU (n/a%)
===End Milestore
===Begin Milestore: player_num = 100, map_size = (-1000.000000, 1000.000000)
Add Player (1 times) 0.000288s wall, 0.000000s user + 0.000000s system = 0.000000s CPU (n/a%)
Tick (1 times) 0.000048s wall, 0.000000s user + 0.000000s system = 0.000000s CPU (n/a%)
Update Pos (10 times) 0.000200s wall, 0.000000s user + 0.000000s system = 0.000000s CPU (n/a%)
===End Milestore
===Begin Milestore: player_num = 100, map_size = (-10000.000000, 10000.000000)
Add Player (1 times) 0.000194s wall, 0.000000s user + 0.000000s system = 0.000000s CPU (n/a%)
Tick (1 times) 0.000041s wall, 0.000000s user + 0.000000s system = 0.000000s CPU (n/a%)
Update Pos (10 times) 0.000192s wall, 0.000000s user + 0.000000s system = 0.000000s CPU (n/a%)
===End Milestore
===Begin Milestore: player_num = 1000, map_size = (-50.000000, 50.000000)
Add Player (1 times) 0.130766s wall, 0.130000s user + 0.000000s system = 0.130000s CPU (99.4%)
Tick (1 times) 0.028091s wall, 0.020000s user + 0.000000s system = 0.020000s CPU (71.2%)
Update Pos (10 times) 0.005369s wall, 0.010000s user + 0.000000s system = 0.010000s CPU (186.2%)
===End Milestore
===Begin Milestore: player_num = 1000, map_size = (-100.000000, 100.000000)
Add Player (1 times) 0.103015s wall, 0.100000s user + 0.000000s system = 0.100000s CPU (97.1%)
Tick (1 times) 0.019545s wall, 0.020000s user + 0.000000s system = 0.020000s CPU (102.3%)
Update Pos (10 times) 0.009208s wall, 0.010000s user + 0.000000s system = 0.010000s CPU (108.6%)
===End Milestore
===Begin Milestore: player_num = 1000, map_size = (-1000.000000, 1000.000000)
Add Player (1 times) 0.010150s wall, 0.010000s user + 0.000000s system = 0.010000s CPU (98.5%)
Tick (1 times) 0.000845s wall, 0.000000s user + 0.000000s system = 0.000000s CPU (n/a%)
Update Pos (10 times) 0.003023s wall, 0.000000s user + 0.000000s system = 0.000000s CPU (n/a%)
===End Milestore
===Begin Milestore: player_num = 1000, map_size = (-10000.000000, 10000.000000)
Add Player (1 times) 0.004950s wall, 0.010000s user + 0.000000s system = 0.010000s CPU (202.0%)
Tick (1 times) 0.000427s wall, 0.000000s user + 0.000000s system = 0.000000s CPU (n/a%)
Update Pos (10 times) 0.002234s wall, 0.000000s user + 0.000000s system = 0.000000s CPU (n/a%)
===End Milestore
===Begin Milestore: player_num = 10000, map_size = (-50.000000, 50.000000)
Add Player (1 times) 21.606402s wall, 21.040000s user + 0.570000s system = 21.610000s CPU (100.0%)
Tick (1 times) 3.696885s wall, 3.680000s user + 0.030000s system = 3.710000s CPU (100.4%)
Update Pos (10 times) 0.434396s wall, 0.430000s user + 0.000000s system = 0.430000s CPU (99.0%)
===End Milestore
===Begin Milestore: player_num = 10000, map_size = (-100.000000, 100.000000)
Add Player (1 times) 18.499235s wall, 18.470000s user + 0.020000s system = 18.490000s CPU (100.0%)
Tick (1 times) 2.292608s wall, 2.290000s user + 0.000000s system = 2.290000s CPU (99.9%)
Update Pos (10 times) 1.522617s wall, 1.530000s user + 0.000000s system = 1.530000s CPU (100.5%)
===End Milestore
===Begin Milestore: player_num = 10000, map_size = (-1000.000000, 1000.000000)
Add Player (1 times) 1.642519s wall, 1.640000s user + 0.000000s system = 1.640000s CPU (99.8%)
Tick (1 times) 0.042767s wall, 0.050000s user + 0.000000s system = 0.050000s CPU (116.9%)
Update Pos (10 times) 0.202949s wall, 0.200000s user + 0.000000s system = 0.200000s CPU (98.5%)
===End Milestore
===Begin Milestore: player_num = 10000, map_size = (-10000.000000, 10000.000000)
Add Player (1 times) 0.571257s wall, 0.570000s user + 0.000000s system = 0.570000s CPU (99.8%)
Tick (1 times) 0.006325s wall, 0.010000s user + 0.000000s system = 0.010000s CPU (158.1%)
Update Pos (10 times) 0.042568s wall, 0.040000s user + 0.000000s system = 0.040000s CPU (94.0%)
===End Milestore
Comme nous l'avons analysé, la liste croisée prend plus de temps pour Add Player et Update Pos, en particulier pour Add Player, où sa performance est inférieure de plusieurs centaines, voire des milliers de fois par rapport à la grille (avec 100, [-50, 50], la liste croisée prend 2ms, alors que la grille n'en prend que 0.08ms ; avec 10000, [-50, 50], la liste croisée prend 21.6s, alors que la grille n'en prend que 6ms). Pour Update Pos, le temps d'exécution peut également varier d'une centaine de fois ; avec 10000, [-100, 100], la liste croisée met 1.5s pour mettre à jour la position du joueur, alors que la grille ne prend que 18ms. On peut constater que les limites de temps d'exécution de la liste croisée pour Add Player et Update Pos sont plus larges que celles de la grille. Cela est davantage influencé par le nombre de joueurs et la taille de la carte. Dans les zones densément peuplées, la performance de ces deux opérations chute rapidement jusqu'à devenir inutilisable.
En ce qui concerne l'opération "Tick" du Cross List, sa performance globale est effectivement meilleure que celle de la grille en 9 sections. Dans le meilleur des cas, le temps nécessaire est environ la moitié de celui de la grille en 9 sections ("1000, [-1000, 1000]" le Cross List prend 0,8 ms, tandis que la grille en 9 sections prend 1,8 ms). Cependant, dans le pire des cas, le Cross List peut se dégrader pour atteindre des performances proches de celles de la grille en 9 sections ("10000, [-10000, 10000]" le Cross List prend 3,7 s, contre 3,8 s pour la grille en 9 sections). Cela est dû au fait que, en raison de la petite taille de l'environnement, les joueurs se trouvent tous à portée les uns des autres dans leur zone AOI respective, ce qui fait que la quantité de candidats parcourus par "Tick" dans le Cross List est en fait très proche de celle de la grille en 9 sections.
La utilisation de la grille croisée doit être plus performante que la grille à neuf cases. Cela requiert des hypothèses plus solides, telles que player_num = 1000, map_size = [-1000, 1000]. Dans ce cas, le temps nécessaire pour Tick est de 0.8ms pour la grille croisée et de 1.8ms pour la grille à neuf cases. Quant à Update Pos, il est de 0.3ms pour la grille croisée et de 0.18ms pour la grille à neuf cases (notez que le temps de test de Update Pos est la somme du temps de 10 exécutions). En ce qui concerne le temps total de Tick + Update Pos, pour que la grille croisée soit plus rapide que la grille à neuf cases, le nombre d'occurrences de Update Pos ne doit pas dépasser 8 fois celui de Tick, ou en d'autres termes, entre deux Tick, le nombre d'occurrences de Update Pos doit être inférieur à 8 fois. De plus, en raison du temps considérable nécessaire pour ajouter un joueur à la grille croisée, cette méthodologie n'est pas adaptée pour les situations où les joueurs entrent et sortent fréquemment de la scène en peu de temps, ou lors de téléportations à grande échelle à l'intérieur de la scène. De plus, un grand nombre soudain de joueurs entrant dans la scène peut également entraîner une dégradation des performances et une utilisation intensive du processeur.
Pour les listes de hachage croisées, une optimisation peut encore être réalisée sous une certaine condition : éliminer le Tick, à condition que le jeu puisse accepter des AOI carrés et que les autres consumptions, notamment réseau, induites par les AOI carrés soient acceptables. En réalité, cette condition est assez stricte, car dans le jeu, les coûts liés aux AOI n’occupent généralement qu'une part marginale du CPU, mais passer d'un AOI circulaire à un AOI carré entraîne une augmentation de la surface de l'AOI, ce qui accroît également le nombre de joueurs à l'intérieur de cette zone. Dans une distribution uniforme, le nombre de joueurs pourrait augmenter jusqu'à 1.27 fois par rapport à l'original. Cependant, dès que cette condition est satisfaite, la liste de hachage croisée peut fonctionner sans avoir besoin de Tick pour mettre à jour régulièrement les événements d'AOI, car dans son implémentation, les candidates de la liste de hachage croisée maintiennent déjà un ensemble d'AOI carrés, initialement prévu pour calculer des AOI circulaires, et nécessitant une traversée supplémentaire dans le Tick pour calculer les distances. Dans ce contexte, la liste de hachage croisée peut potentiellement atteindre de très bonnes performances, car les performances de Update Pos peuvent différer du Tick de plusieurs à plusieurs dizaines de fois.
Fournir finalement un histogramme comparatif des deux.
Résumé
Dans ce texte, nous présentons les principes et les mises en œuvre de deux algorithmes AOI (grille en neuf points et chaîne en croix) et analysons les performances de ces deux algorithmes à partir de données mesurées, espérant apporter un peu d'aide ou d'inspiration aux lecteurs.
Dans l'ensemble, la méthode du carré magique est simple à mettre en œuvre, avec des performances équilibrées qui ne se dégradent pas facilement, ce qui en fait un choix idéal pour les jeux où l’AOI n'est pas un goulot d'étranglement. Les fluctuations de performances de la méthode du carré magique se situent dans une fourchette prévisible, avec un seuil de performance relativement élevé, et elle ne conduit pas facilement à des goulots d'étranglement. Cependant, d'un autre côté, l'espace d'optimisation est également limité, et la complexité temporelle est plutôt fixe. En revanche, la méthode de la chaîne croisée est plus complexe à mettre en œuvre, avec un seuil de performance inférieur à celui de la méthode du carré magique. Cependant, si certaines hypothèses et conditions sont satisfaites, l'espace d'optimisation de la chaîne croisée peut être plus important, en d'autres termes, son plafond peut être plus élevé. Les deux méthodes ont leurs avantages et inconvénients ; dans l'industrie du jeu, différentes engines choisissent l'une ou l'autre selon leurs besoins, chacun y trouvant son compte.
Mes compétences sont limitées, le contenu du texte reflète uniquement mes opinions. Si vous remarquez des lacunes ou des erreurs, n'hésitez pas à laisser un commentaire pour en discuter.
Original: https://wiki.disenone.site/fr
This post is protected by CC BY-NC-SA 4.0 agreement, should be reproduced with attribution.
Visitors. Total Visits. Page Visits.
Ce message a été traduit avec ChatGPT, merci de laisser un retourVeuillez indiquer toute omission.