ゲーム AOI アルゴリズム解析と性能実測
引子
AOI(関心領域)は、マルチプレイヤーオンラインゲームにおいて非常に基本的な機能であり、プレイヤーは視野範囲内に入る他のプレイヤーやエンティティの情報を受け取る必要があります。プレイヤーの視野範囲内にどのエンティティが存在するか、どのエンティティが視野に入ったり出たりするかを計算するアルゴリズムを、一般に AOI アルゴリズムと呼びます。
本文では、九宮格と十字鏈の2種類の AOI アルゴリズムについて論じ、それらの実測パフォーマンスを分析しています。これにより、理解を深め、問題に直面しても落ち着いて対処できるようにしています。
文中では、プレイヤーとエンティティという2つの用語が言及されます。エンティティはゲーム内のオブジェクトの概念であり、プレイヤーはAOIを持つエンティティです。
文中のコードはここで見つけることができます:AoiTestingI'm sorry, but there is no text to translate.
九宮格
いわゆる九宮格とは、シーン内のすべてのエンティティの位置をグリッドに分割することを指し、例えば辺の長さが200の正方形に分割します。中心のプレイヤーのAOI範囲内にある他のエンティティを見つけるために、この範囲内で関係するグリッド内のプレイヤーを全て比較します。
例えば、シーンごとに100ミリ秒ごとにTickが発生し、そのTickの中でプレイヤーのAOIを以下のように更新できます:
プレイヤーの位置を中心にして、AOI半径に関連するグリッドの集合を計算します。 格子セット内の実体とプレイヤーとの距離を個別に計算します。 AOI 半径よりも距離が短い実体の集合がプレイヤーの新しい AOI となります。
九宮格アルゴリズムは非常にシンプルに実装できます。アルゴリズムは数文で明確に説明できますが、具体的な性能分析は後に回し、まずは十字連結リストアルゴリズムを見てみましょう。
十字リンクリスト
3Dゲームでは、通常、X軸とZ軸の座標に対して整列されたリストを作成します。各エンティティはリスト上にノードを持ち、そのノードには座標軸の値が格納されます。値が増加する順に配置されます。ただし、エンティティの座標だけを保存する場合、これらの2つのリストはまだ効率的な検索を提供しません。
本当のポイントは、リンクされたリストに、AOIを持つプレイヤーごとに左右に2つのセンチネルノードを追加することです。2つのセンチネルの座標値は、プレイヤー自体の座標とちょうどAOI半径だけ異なります。例えば、プレイヤー P の座標が (a, b, c) で、AOI半径が r の場合、X軸上には2つのセンチネル left_x, right_x があり、それぞれの座標値は a - r および a + r になります。センチネルが存在するため、他のエンティティノードとの移動を追跡してAOIを更新します。前述の例を続けると、エンティティ E がX軸で左から右に left_x を越えて left_x の左側に来る動きをすると、E は確実に P のAOIを離れたことになります。同様に、right_x を越えて右側に行った場合もAOIを離れたことになります。逆に、left_x を越えて右側に行った場合、または right_x を越えて左側に行った場合は、P のAOIに入る可能性があることを意味します。
見るとわかるように、十字リンクリストのアルゴリズムは九宮格よりも複雑です。私たちは2つの順序付きリストを維持する必要があり、各エンティティの座標が更新されるたびに、リスト上のノードを同期して移動する必要があります。その際、他のノードを越えて移動する際に、AOIを更新する必要があります。
九宫格の実現
実測の性能に関わるため、まずは九宮格アルゴリズムの実装の詳細について少し掘り下げてみましょう:
struct Sensor {
// ...
Nuid sensor_id;
float radius;
float radius_square;
PlayerPtrList aoi_players[2];
};
struct PlayerAoi {
// ...
Nuid nuid;
SquareId square_id;
int square_index;
Pos pos;
Pos last_pos;
Uint32 flags;
std::vector<Sensor> sensors;
};
PlayerAoi にはプレイヤーのデータが保存されており、sensors 配列があります。sensors は一定範囲内のエンティティを計算するためのもので、各Tick 後に計算されたエンティティはaoi_players に配置されます。aoi_players には、前回のTick の結果と比較するための2つの配列が保存され、プレイヤーの出入りを求めます。Tick の大まかな流れは次のようになります:
AoiUpdateInfos SquareAoi::Tick() {
AoiUpdateInfos update_infos;
PlayerPtrList remove_list;
for (auto& elem : player_map_) {
auto& player = *elem.second;
// ...
// センサーを持つプレイヤーに対して Aoi を計算する
if (!player.sensors.empty()) {
auto update_info = _UpdatePlayerAoi(cur_aoi_map_idx_, &player);
if (!update_info.sensor_update_list.empty()) {
update_infos.emplace(update_info.nuid, std::move(update_info));
}
}
// ...
}
// ...
// プレーヤーの前回の位置を記録する
for (auto& elem : player_map_) {
auto& player = *elem.second;
player.last_pos = player.pos;
}
cur_aoi_map_idx_ = 1 - cur_aoi_map_idx_;
return update_infos;
}
「Tick」で行われる作業は非常にシンプルで、sensors を持つプレイヤーを順に検索し、一つずつ sensor の範囲内に存在するエンティティを計算して AOI としています。 last_pos は、エンティティがAOIに進入したか離れたかを判断に使われます。 _UpdatePlayerAoi のコードは以下の通りです:
AoiUpdateInfo SquareAoi::_UpdatePlayerAoi(Uint32 cur_aoi_map_idx, PlayerAoi* pptr) {
AoiUpdateInfo aoi_update_info;
aoi_update_info.nuid = pptr->nuid;
Uint32 new_aoi_map_idx = 1 - cur_aoi_map_idx;
for (auto& sensor : pptr->sensors) {
auto& old_aoi = sensor.aoi_players[cur_aoi_map_idx];
auto& new_aoi = sensor.aoi_players[new_aoi_map_idx];
(this->*calc_aoi_players_func_)(*pptr, sensor, &new_aoi);
SensorUpdateInfo update_info;
auto& enters = update_info.enters;
auto& leaves = update_info.leaves;
float radius_square = sensor.radius_square;
_CheckLeave(pptr, radius_square, old_aoi, &leaves);
_CheckEnter(pptr, radius_square, new_aoi, &enters);
if (enters.empty() && leaves.empty()) {
continue;
}
update_info.sensor_id = sensor.sensor_id;
aoi_update_info.sensor_update_list.push_back(std::move(update_info));
}
return aoi_update_info;
}
old_aoi は前回の Tick に基づいて計算された AOI であり、new_aoi は今回の Tick で計算する必要がある AOI です。new_aoi は AOI 範囲内のすべてのグリッドに存在するエンティティを遍歴し、プレイヤーとの距離が AOI 半径未満のエンティティを選出することで得られます。その後、_CheckLeave と _CheckEnter の2つの関数を使用して、今回の Tick における AOI からの離脱および AOI への入場を計算します。たとえば、new_aoi 内のエンティティ last_pos が AOI 範囲外にある場合、これはそのエンティティが今回の Tick に AOI 範囲に入ったことを示します。具体的なコードはソースファイルを参照してください。ここでは詳細を述べることは控えます。
十字リンクリストの実装
九宫格に比べて、十字連結リストは実装がより複雑です。ます基本的なデータ構造を見てみましょう:
struct CoordNode {
// ...
Uint8 type;
float value;
CoordNode *prev = nullptr;
CoordNode *next = nullptr;
PlayerAoi *pplayer;
Sensor *psensor;
};
KHASH_MAP_INIT_INT64(SensorHashMap, PlayerAoi*);
struct Sensor {
// ...
Nuid sensor_id;
float radius;
float radius_square;
PlayerAoi *pplayer;
CoordNode left_x;
CoordNode right_x;
CoordNode left_z;
CoordNode right_z;
PlayerPtrList aoi_players[2];
std::shared_ptr<khash_t(SensorHashMap)> aoi_player_candidates;
};
struct PlayerAoi {
// ...
Nuid nuid;
Pos pos;
Pos last_pos;
Uint32 flags;
CoordNode node_x;
CoordNode node_z;
std::vector<Sensor> sensors;
std::shared_ptr<boost::unordered_map<Nuid, std::vector<Nuid>>> detected_by;
};
Sensor と PlayerAoi は九宮格に似ていますが、CoordNode というリンクリストに関連するノード構造が追加されています。CoordNode はリンクリスト上のノードであり、自身の種類と値を記録しています。種類には3種類があります:プレイヤーノード、Sensor の左ノード、Sensor の右ノード。
十字链表の大部分の作業は、リストの順序を維持することにあります:
プレーヤーが参加する際には、プレーヤーノードを整然とした位置に移動し、プレーヤーノードを移動する際に他のプレーヤーのAOIイベントの入退を処理します。
* プレイヤーが正しい位置に移動すると、Sensor の左右ノードはプレイヤーの前後の位置から出発し、正しい位置に移動します。また、他のプレイヤーノードを越えた際に発生する入退室イベントを処理します。
プレイヤーが移動すると、プレイヤーの座標が更新され、Sensor ノードとその左右ノードが移動し、AOI の進入と退出が処理されます。
移動ノードのコードは以下のとおりです。ノードを一つ越えるごとに、MoveCross 関数が一度呼び出され、MoveCross 関数は移動方向や越えたノードのタイプに基づいて、AOIに入るか出るかを決定します。
void ListUpdateNode(CoordNode **list, CoordNode *pnode) {
float value = pnode->value;
if (pnode->next && pnode->next->value < value) {
// move right
auto cur_node = pnode->next;
while (1) {
MoveCross(MOVE_DIRECTION_RIGHT, pnode, cur_node);
if (!cur_node->next || cur_node->next->value >= value) break;
cur_node = cur_node->next;
}
ListRemove(list, pnode);
ListInsertAfter(list, cur_node, pnode);
} else if (pnode->prev && pnode->prev->value > value) {
// move left
auto cur_node = pnode->prev;
while (1) {
MoveCross(MOVE_DIRECTION_LEFT, pnode, cur_node);
if (!cur_node->prev || cur_node->prev->value <= value) break;
cur_node = cur_node->prev;
}
ListRemove(list, pnode);
ListInsertBefore(list, cur_node, pnode);
}
}
リンクリストの移動は非常に遅く、複雑度は O(n) です。特にプレイヤーが新たにシーンに参加する際、プレイヤーは無限遠方から正しい位置に徐々に移動する必要があり、そのために多くのノードを遍歴し、大きなリソースを消費します。パフォーマンスを最適化するために、シーン内に固定位置で灯台を設置することができます。この灯台の処理はプレイヤーとほぼ同じですが、プレイヤーよりも1つ多くの detected_by データを記録しています。detected_by は、その哨兵エンティティがどの Sensor の範囲内にいるかを記録するためのものです。プレイヤーが初めてシーンに入るとき、最も遠い場所から移動を始めるのではなく、最近の灯台を見つけ、その灯台の近くにノードを挿入します。そして、灯台にある detected_by データを通じて、灯台と一致する他のプレイヤーの AOI 範囲に素早く入って、正しい位置に移動を始めます。当然、移動中には出入りの処理も行う必要があります。同様に、Sensor に関しても、最初に灯台のデータを継承し、そこから正しい位置へ移動することが可能です。この2つの最適化を通じて、プレイヤー挿入のパフォーマンスを1倍以上向上させることができます。
Sensor には aoi_player_candidates という名前の HashMap があります(ここではパフォーマンスのために、khash)。ノードの移動によって引き起こされるAOIイベントは、実際にはX-Z座標軸上の辺が 2r の正方形領域しか検出できません。厳密な意味での円形領域のAOIではありません。この正方形領域内のエンティティはすべて aoi_player_candidates に記録され、Tick 中に円形領域内のAOI範囲を計算し、それを candidates と呼びます。
十字リンクリストの操作は、正方形の領域内のエンティティcandidatesを常に維持するために行われます。十字リンクリスト内でのTickの操作は、ほぼ九宮格と一致しますが、AOIのcandidatesを遍歴計算する際の内容は異なります。九宮格のcandidatesは、AOIの円形領域がカバーするグリッドのエンティティであり、十字リンクリストはSensorの左右のノードによって定義される一辺の長さが2rの正方形領域内のエンティティで構成されています。定性的に言えば、十字リンクリストのcandidatesは一般的に九宮格よりも少ないため、Tickの遍歴回数が少なく、性能が優れます。ただし、十字リンクリストにはリストの維持に大量の追加な性能消費がかかります。これらの全体的な性能の優劣については、今後実測してみましょう。
性能実測
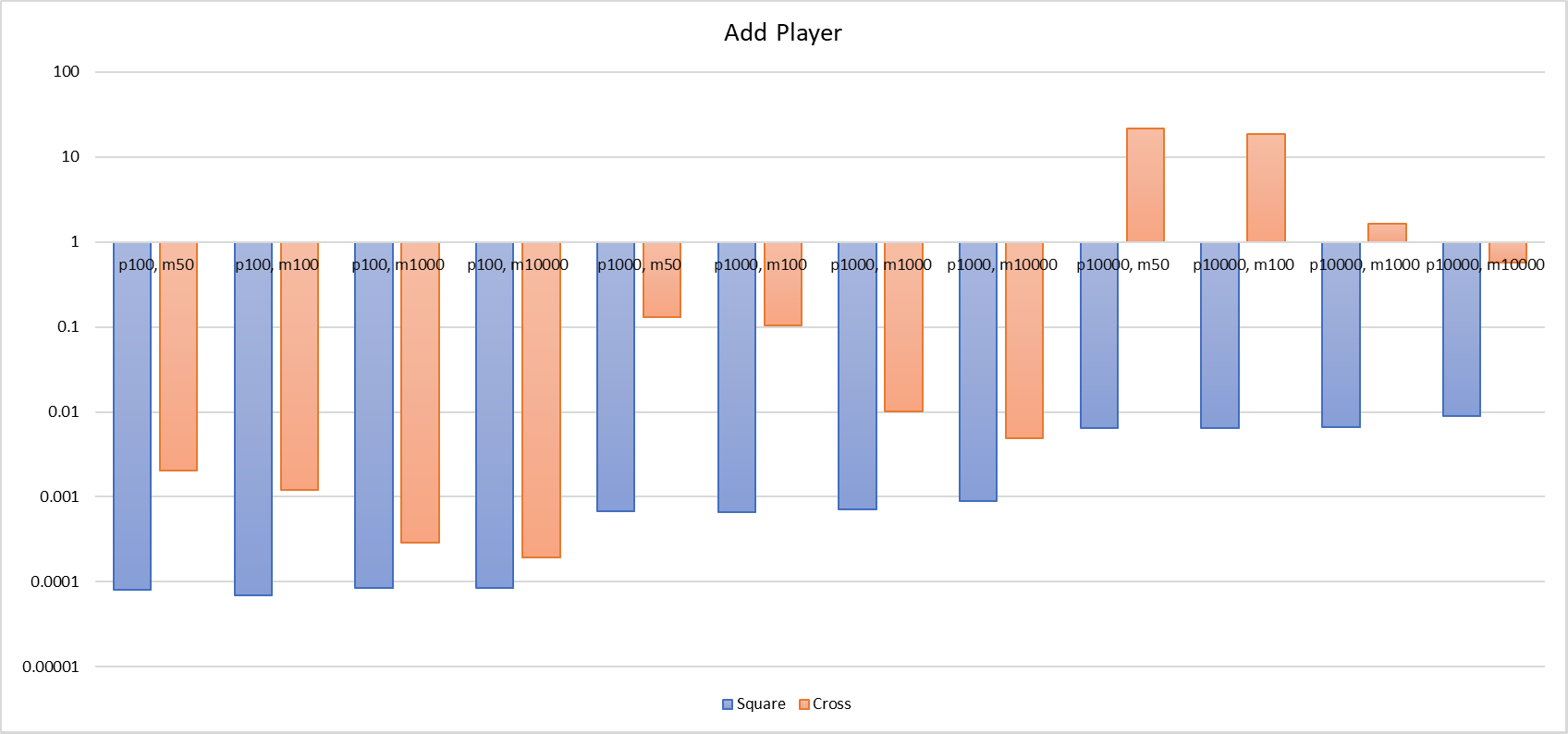
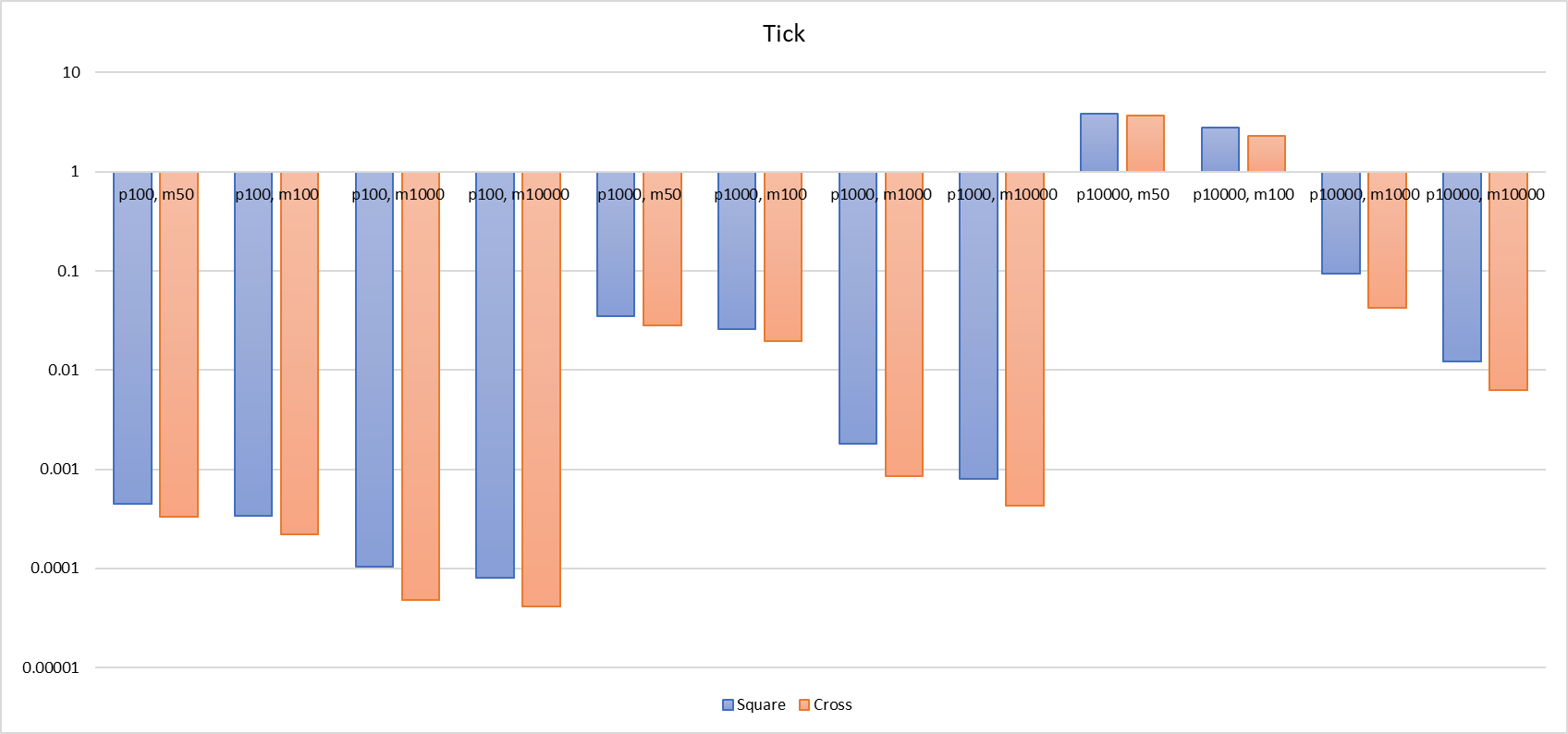
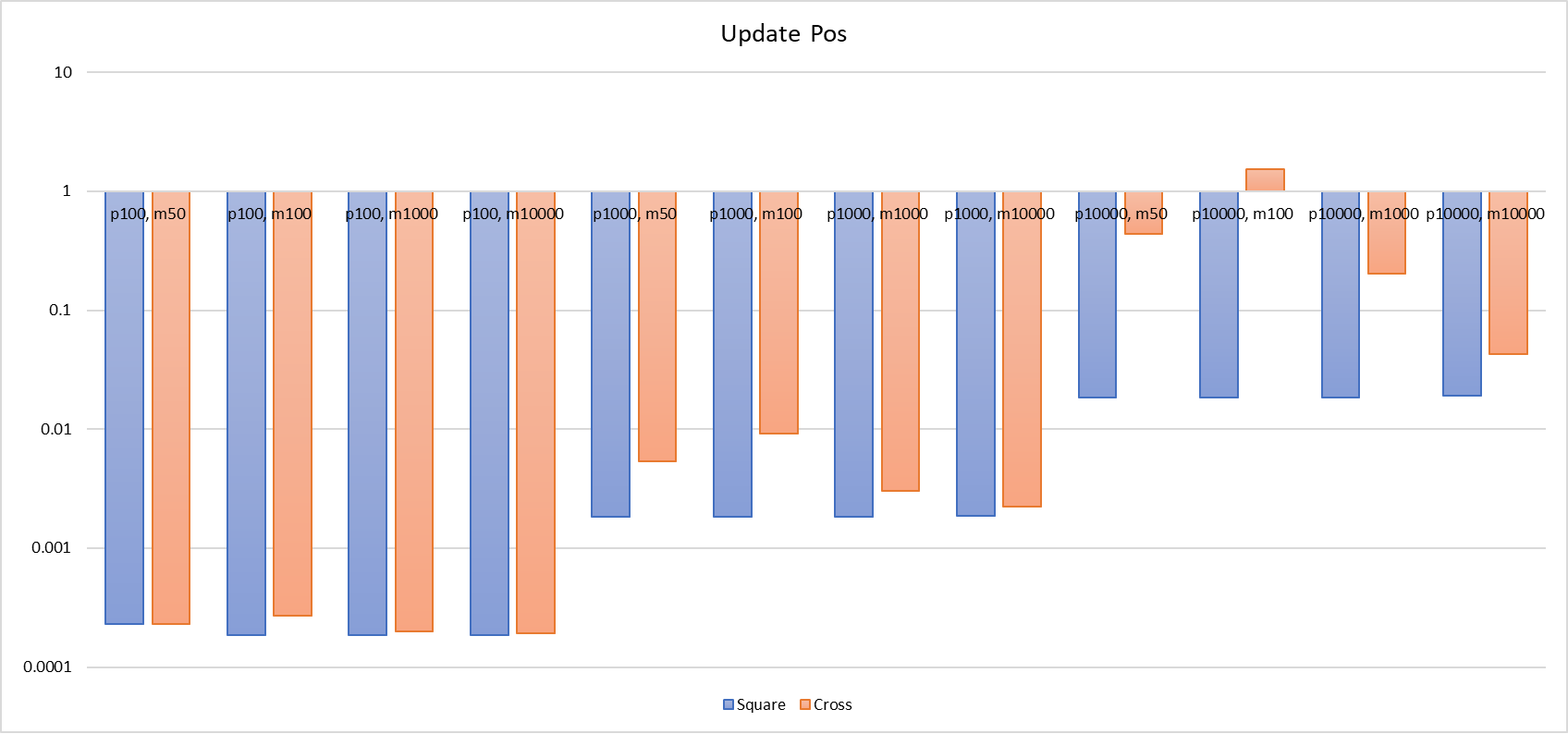
こちらでは、プレイヤーがシーンに追加される時間(Add Player)、AOIの進入および退出イベントの計算時間(Tick)、プレイヤーの位置座標の更新時間(Update Pos)をそれぞれ計測しました。
プレイヤーの初期位置はマップの範囲内でランダムに生成され、その後プレイヤーがシーンに追加されます。player_num はプレイヤーの数を示し、map_size はマップの X-Z 座標軸の範囲を表します。プレイヤーの位置はこの範囲内で均等にランダムに生成され、各プレイヤーには半径 100 の Sensor が AOI として設定されています。計算時間には boost::timer::cpu_timer が使用されています。player_num はそれぞれ 100, 1000, 10000 の3つのケースが選ばれ、一方 map_size には [-50, 50], [-100, 100], [-1000, 1000], [-10000, 10000] の4つのケースが選ばれました。
プレイヤーの位置を更新すると、プレイヤーはランダムな方向に向かって、速度6m/sで移動します。
本次测试环境为:
- CPU: Intel(R) Core(TM) i5-4590 CPU @ 3.30GHz
- システム: Debian GNU/Linux 10 (buster)
- gcc バージョン: gcc version 8.3.0 (Debian 8.3.0-6) boost 版本: boost_1_75_0
九宮格実測
九宮格のテスト結果は以下の通りです:
===Begin Milestore: player_num = 100, map_size = (-50.000000, 50.000000)
Add Player (1 times) 0.000081s wall, 0.000000s user + 0.000000s system = 0.000000s CPU (n/a%)
Tick (1 times) 0.000452s wall, 0.000000s user + 0.000000s system = 0.000000s CPU (n/a%)
Update Pos (10 times) 0.000230s wall, 0.000000s user + 0.000000s system = 0.000000s CPU (n/a%)
===End Milestore
===Begin Milestore: player_num = 100, map_size = (-100.000000, 100.000000)
Add Player (1 times) 0.000070s wall, 0.000000s user + 0.000000s system = 0.000000s CPU (n/a%)
Tick (1 times) 0.000338s wall, 0.000000s user + 0.000000s system = 0.000000s CPU (n/a%)
Update Pos (10 times) 0.000185s wall, 0.000000s user + 0.000000s system = 0.000000s CPU (n/a%)
===End Milestore
===Begin Milestore: player_num = 100, map_size = (-1000.000000, 1000.000000)
Add Player (1 times) 0.000084s wall, 0.000000s user + 0.000000s system = 0.000000s CPU (n/a%)
Tick (1 times) 0.000103s wall, 0.000000s user + 0.000000s system = 0.000000s CPU (n/a%)
Update Pos (10 times) 0.000187s wall, 0.000000s user + 0.000000s system = 0.000000s CPU (n/a%)
===End Milestore
===Begin Milestore: player_num = 100, map_size = (-10000.000000, 10000.000000)
Add Player (1 times) 0.000084s wall, 0.000000s user + 0.000000s system = 0.000000s CPU (n/a%)
Tick (1 times) 0.000080s wall, 0.000000s user + 0.000000s system = 0.000000s CPU (n/a%)
Update Pos (10 times) 0.000185s wall, 0.000000s user + 0.000000s system = 0.000000s CPU (n/a%)
===End Milestore
===Begin Milestore: player_num = 1000, map_size = (-50.000000, 50.000000)
Add Player (1 times) 0.000673s wall, 0.000000s user + 0.000000s system = 0.000000s CPU (n/a%)
Tick (1 times) 0.035298s wall, 0.030000s user + 0.000000s system = 0.030000s CPU (85.0%)
Update Pos (10 times) 0.001841s wall, 0.000000s user + 0.000000s system = 0.000000s CPU (n/a%)
===End Milestore
===Begin Milestore: player_num = 1000, map_size = (-100.000000, 100.000000)
Add Player (1 times) 0.000664s wall, 0.000000s user + 0.000000s system = 0.000000s CPU (n/a%)
Tick (1 times) 0.025806s wall, 0.030000s user + 0.000000s system = 0.030000s CPU (116.3%)
Update Pos (10 times) 0.001842s wall, 0.000000s user + 0.000000s system = 0.000000s CPU (n/a%)
===End Milestore
===Begin Milestore: player_num = 1000, map_size = (-1000.000000, 1000.000000)
Add Player (1 times) 0.000721s wall, 0.000000s user + 0.000000s system = 0.000000s CPU (n/a%)
Tick (1 times) 0.001793s wall, 0.000000s user + 0.000000s system = 0.000000s CPU (n/a%)
Update Pos (10 times) 0.001849s wall, 0.010000s user + 0.000000s system = 0.010000s CPU (540.8%)
===End Milestore
===Begin Milestore: player_num = 1000, map_size = (-10000.000000, 10000.000000)
Add Player (1 times) 0.000885s wall, 0.000000s user + 0.000000s system = 0.000000s CPU (n/a%)
Tick (1 times) 0.000804s wall, 0.000000s user + 0.000000s system = 0.000000s CPU (n/a%)
Update Pos (10 times) 0.001855s wall, 0.000000s user + 0.000000s system = 0.000000s CPU (n/a%)
===End Milestore
===Begin Milestore: player_num = 10000, map_size = (-50.000000, 50.000000)
Add Player (1 times) 0.006454s wall, 0.010000s user + 0.000000s system = 0.010000s CPU (154.9%)
Tick (1 times) 3.822028s wall, 3.800000s user + 0.020000s system = 3.820000s CPU (99.9%)
Update Pos (10 times) 0.018402s wall, 0.020000s user + 0.000000s system = 0.020000s CPU (108.7%)
===End Milestore
===Begin Milestore: player_num = 10000, map_size = (-100.000000, 100.000000)
Add Player (1 times) 0.006439s wall, 0.000000s user + 0.000000s system = 0.000000s CPU (n/a%)
Tick (1 times) 2.805551s wall, 2.760000s user + 0.040000s system = 2.800000s CPU (99.8%)
Update Pos (10 times) 0.018489s wall, 0.010000s user + 0.000000s system = 0.010000s CPU (54.1%)
===End Milestore
===Begin Milestore: player_num = 10000, map_size = (-1000.000000, 1000.000000)
Add Player (1 times) 0.006698s wall, 0.010000s user + 0.000000s system = 0.010000s CPU (149.3%)
Tick (1 times) 0.093759s wall, 0.100000s user + 0.000000s system = 0.100000s CPU (106.7%)
Update Pos (10 times) 0.018350s wall, 0.010000s user + 0.000000s system = 0.010000s CPU (54.5%)
===End Milestore
===Begin Milestore: player_num = 10000, map_size = (-10000.000000, 10000.000000)
Add Player (1 times) 0.009046s wall, 0.010000s user + 0.000000s system = 0.010000s CPU (110.6%)
Tick (1 times) 0.012091s wall, 0.010000s user + 0.000000s system = 0.010000s CPU (82.7%)
Update Pos (10 times) 0.019033s wall, 0.020000s user + 0.000000s system = 0.020000s CPU (105.1%)
===End Milestore
プレイヤーが100人の場合、九宮格は三つの操作とも非常に効率的で、限界状況ではmap_size = [-50, 50]、すべてのプレイヤーが互いにAOI範囲内にいる状態で、Tickにかかる時間は約0.4msです。プレイヤーのシーンへの参加と座標の更新はともに線形計算であり、性能は非常に優れています。プレイヤー数が1万人、map_size = [-50, 50]の場合、Add PlayerとUpdate Posはいずれも線形計算なので、数ミリ秒で完了しますが、Tickにかかる時間が3.8sに増え、大量のCPUリソースを必要とするため使用できなくなります。1万人のプレイヤーとmap_size = [-1000, 1000]の場合、Tickは約94msかかります。Tick周波数を下げることができれば、例えば1秒に2回の場合、まだ使用可能な範囲に属します。
十字链表の実測
十字链表のテスト結果は次のとおりです:
===Begin Milestore: player_num = 100, map_size = (-50.000000, 50.000000)
Add Player (1 times) 0.002057s wall, 0.000000s user + 0.000000s system = 0.000000s CPU (n/a%)
Tick (1 times) 0.000330s wall, 0.000000s user + 0.000000s system = 0.000000s CPU (n/a%)
Update Pos (10 times) 0.000232s wall, 0.000000s user + 0.000000s system = 0.000000s CPU (n/a%)
===End Milestore
===Begin Milestore: player_num = 100, map_size = (-100.000000, 100.000000)
Add Player (1 times) 0.001201s wall, 0.000000s user + 0.000000s system = 0.000000s CPU (n/a%)
Tick (1 times) 0.000222s wall, 0.000000s user + 0.000000s system = 0.000000s CPU (n/a%)
Update Pos (10 times) 0.000272s wall, 0.000000s user + 0.000000s system = 0.000000s CPU (n/a%)
===End Milestore
===Begin Milestore: player_num = 100, map_size = (-1000.000000, 1000.000000)
Add Player (1 times) 0.000288s wall, 0.000000s user + 0.000000s system = 0.000000s CPU (n/a%)
Tick (1 times) 0.000048s wall, 0.000000s user + 0.000000s system = 0.000000s CPU (n/a%)
Update Pos (10 times) 0.000200s wall, 0.000000s user + 0.000000s system = 0.000000s CPU (n/a%)
===End Milestore
===Begin Milestore: player_num = 100, map_size = (-10000.000000, 10000.000000)
Add Player (1 times) 0.000194s wall, 0.000000s user + 0.000000s system = 0.000000s CPU (n/a%)
Tick (1 times) 0.000041s wall, 0.000000s user + 0.000000s system = 0.000000s CPU (n/a%)
Update Pos (10 times) 0.000192s wall, 0.000000s user + 0.000000s system = 0.000000s CPU (n/a%)
===End Milestore
===Begin Milestore: player_num = 1000, map_size = (-50.000000, 50.000000)
Add Player (1 times) 0.130766s wall, 0.130000s user + 0.000000s system = 0.130000s CPU (99.4%)
Tick (1 times) 0.028091s wall, 0.020000s user + 0.000000s system = 0.020000s CPU (71.2%)
Update Pos (10 times) 0.005369s wall, 0.010000s user + 0.000000s system = 0.010000s CPU (186.2%)
===End Milestore
===Begin Milestore: player_num = 1000, map_size = (-100.000000, 100.000000)
Add Player (1 times) 0.103015s wall, 0.100000s user + 0.000000s system = 0.100000s CPU (97.1%)
Tick (1 times) 0.019545s wall, 0.020000s user + 0.000000s system = 0.020000s CPU (102.3%)
Update Pos (10 times) 0.009208s wall, 0.010000s user + 0.000000s system = 0.010000s CPU (108.6%)
===End Milestore
===Begin Milestore: player_num = 1000, map_size = (-1000.000000, 1000.000000)
Add Player (1 times) 0.010150s wall, 0.010000s user + 0.000000s system = 0.010000s CPU (98.5%)
Tick (1 times) 0.000845s wall, 0.000000s user + 0.000000s system = 0.000000s CPU (n/a%)
Update Pos (10 times) 0.003023s wall, 0.000000s user + 0.000000s system = 0.000000s CPU (n/a%)
===End Milestore
===Begin Milestore: player_num = 1000, map_size = (-10000.000000, 10000.000000)
Add Player (1 times) 0.004950s wall, 0.010000s user + 0.000000s system = 0.010000s CPU (202.0%)
Tick (1 times) 0.000427s wall, 0.000000s user + 0.000000s system = 0.000000s CPU (n/a%)
Update Pos (10 times) 0.002234s wall, 0.000000s user + 0.000000s system = 0.000000s CPU (n/a%)
===End Milestore
===Begin Milestore: player_num = 10000, map_size = (-50.000000, 50.000000)
Add Player (1 times) 21.606402s wall, 21.040000s user + 0.570000s system = 21.610000s CPU (100.0%)
Tick (1 times) 3.696885s wall, 3.680000s user + 0.030000s system = 3.710000s CPU (100.4%)
Update Pos (10 times) 0.434396s wall, 0.430000s user + 0.000000s system = 0.430000s CPU (99.0%)
===End Milestore
===Begin Milestore: player_num = 10000, map_size = (-100.000000, 100.000000)
Add Player (1 times) 18.499235s wall, 18.470000s user + 0.020000s system = 18.490000s CPU (100.0%)
Tick (1 times) 2.292608s wall, 2.290000s user + 0.000000s system = 2.290000s CPU (99.9%)
Update Pos (10 times) 1.522617s wall, 1.530000s user + 0.000000s system = 1.530000s CPU (100.5%)
===End Milestore
===Begin Milestore: player_num = 10000, map_size = (-1000.000000, 1000.000000)
Add Player (1 times) 1.642519s wall, 1.640000s user + 0.000000s system = 1.640000s CPU (99.8%)
Tick (1 times) 0.042767s wall, 0.050000s user + 0.000000s system = 0.050000s CPU (116.9%)
Update Pos (10 times) 0.202949s wall, 0.200000s user + 0.000000s system = 0.200000s CPU (98.5%)
===End Milestore
===Begin Milestore: player_num = 10000, map_size = (-10000.000000, 10000.000000)
Add Player (1 times) 0.571257s wall, 0.570000s user + 0.000000s system = 0.570000s CPU (99.8%)
Tick (1 times) 0.006325s wall, 0.010000s user + 0.000000s system = 0.010000s CPU (158.1%)
Update Pos (10 times) 0.042568s wall, 0.040000s user + 0.000000s system = 0.040000s CPU (94.0%)
===End Milestore
私たちの分析によると、Add PlayerとUpdate Posにおいて、十字リストは時間がかかる傾向にありますが、特にAdd Playerにおいて、パフォーマンスは九宮格と比べて数百倍から何千倍も低くなります(100、[-50、50]の場合、十字リストは2msであるのに対し、九宮格はわずか0.08msです。10000、[-50、50]の場合、十字リストは21.6sで、九宮格はわずか6msです。Update Posの場合も、最大で数百倍の差が出ることがあり、10000、[-100、100]の場合、十字リストのプレイヤー位置更新には1.5sかかりますが、九宮格では18msです。明らかに、十字リストは、九宮格よりもAdd PlayerとUpdate Posの時間範囲が広く、人数やマップサイズの影響を受けやすく、プレイヤー密集地域ではこれらの操作のパフォーマンスが急速に低下し、最終的には使用できなくなります。
十字链Tick操作的性能总体表现确实比九宫格要好,最佳情况下所需时间大约只有九宫格的一半左右(在1000, [-1000, 1000]的情况下,十字链耗时为0.8ms,而九宫格为1.8ms)。但是在最糟糕的情况下,十字链的表现会退化到与九宫格接近(在10000, [-10000, 10000]的情况下,十字链耗时为3.7s,而九宫格为3.8s)。这是因为在小场景中,玩家都在彼此的AOI范围内,导致十字链Tick遍历的候选对象数量实际上已经与九宫格非常接近了。
クロスリンクを九宮格よりも優れた性能で使用するには、より強力な前提条件が必要です。たとえば、 player_num = 1000, map_size = [-1000, 1000] の場合、Tick の処理時間はクロスリンクが 0.8ms で九宮格が 1.8ms、Update Pos ではクロスリンクが 0.3ms で九宮格が 0.18ms となります(Update Pos のテスト時間は 10回 実行した合計)。Tick + Update Pos の合計時間において、クロスリンクが九宮格より短縮するためには、 Update Pos の回数が Tick の 8倍 を超えてはならず、また、2つの Tick の間における Update Pos の回数は 8回未満 である必要があります。さらに、クロスリンクの Add Player は処理時間が非常に長いため、短時間で頻繁にプレイヤーがシーンに出入りしたり、大規模なシーン内で移動する場合には適していません。また、短時間で多くのプレイヤーがシーンに参入した場合も、性能の低下やCPUの大幅な使用を引き起こす可能性があります。
クロスリンクリストについて、1つの前提のもとで最適化が可能です。それは、Tickを排除することで、前提としてゲームが正方形のAOIを受け入れ、正方形AOIによってもたらされるネットワークなどの消費が許容される必要があります。実際、この前提は非常に厳しいものです。なぜなら、ゲーム内でAOIの課金によってCPUが占める割合は通常それほど大きくないのですが、円形AOIを正方形AOIに変更することでAOIの範囲面積が増加し、範囲内のプレイヤー数も増加します。均一に分布した場合、プレイヤー数は元の1.27倍に増える可能性があります。しかし、一旦この前提を満たせれば、クロスリンクリストはAOIイベントを定期的に更新するためにTickを必要としなくなります。なぜなら、クロスリンクリストのcandidatesは正方形のAOIを維持しており、元々は円形AOIを計算するためだけに存在していたため、Tick内で距離を計算するために再度遍歴する必要がなくなるからです。このような状況下では、クロスリンクは素晴らしいパフォーマンスを発揮する可能性があります。なぜなら、クロスリンクリストのUpdate PosのパフォーマンスはTickと比べて数倍から数十倍の差が出ることがあるからです。
最後に、両者の比較を示す棒グラフを示します:
まとめ
本文では、2つのAOIアルゴリズム(九宮格と十字リンク)の原理と基本的な実装について紹介し、実測データを通じてこれらのアルゴリズムの性能を分析しました。読者にとって何らかの助けやインスピレーションをもたらすことができれば幸いです。
全体的に見て、九宮格法は実装が簡単で、性能のバランスが良く落ちることが少ないため、AOIが性能のボトルネックでないゲームに非常に適しています。九宮格法の性能の変動範囲は予測可能で、性能の下限は比較的高く、ボトルネックを引き起こすことも少ないです。しかし、一方で最適化の余地もあまり大きくなく、時間の計算量は比較的固定されています。それに対して十字連鎖法は実装がより複雑で、性能の下限は九宮格法よりも低いですが、いくつかの仮定や前提を満たすことができれば、十字連鎖法はより高い最適化の余地を持っています。言い換えれば、その上限はより高くなり得るということです。この二つの方法にはそれぞれの利点と欠点があり、ゲーム業界では異なるエンジンがそれぞれの方法のいずれかを選択し、自分たちのニーズに応じています。
本人の能力には限界があり、文中の内容はあくまで私の考えを示したものです。至らない点や不適切な部分があれば、ぜひコメントでご指摘ください。
Original: https://wiki.disenone.site/ja
This post is protected by CC BY-NC-SA 4.0 agreement, should be reproduced with attribution.
Visitors. Total Visits. Page Visits.
この投稿はChatGPTを使用して翻訳されました。フィードバック中指出することのない遺漏はない。